R in Finance

Eran Raviv

June 2, 2018

Three parts to this talk

  1. On the ForecastComb package
  2. Other things combinations
  3. How the ForecastComb came to be

Part 1
The ForecastComb package

Start with an example

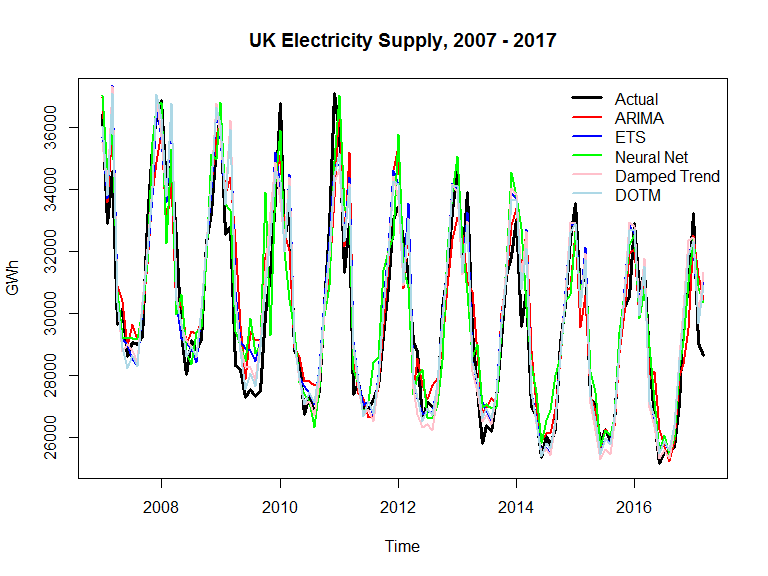
Data preparation

train.obs <- electricity[1:84, 6]
train.pred <- electricity[1:84, 1:5]
test.obs <- electricity[85:123, 6]
test.pred <- electricity[85:123, 1:5]

input_data <- foreccomb(train.obs, train.pred, 
                        test.obs, test.pred)

Individual performance

indi_perf <- matrix(nrow = 5, ncol = 2)
colnames(indi_perf) <- c("Train", "Test")
rownames(indi_perf) <- input_data$modelnames
for (i in 1:5){
  indi_perf[i, 1] <- RMSE(train.pred[,i], train.obs)
  indi_perf[i, 2] <- RMSE(test.pred[,i], test.obs)
}
Train Test
arima 1.24 0.99
ets 1.17 0.87
nnet 1.27 0.98
dampedt 1.18 0.92
dotm 1.04 0.77

“…combining multiple forecasts leads to increased forecast accuracy. In many cases one can make dramatic performance improvements by simply averaging the forecasts.” (source: Forecasting: Principles and Practice. Rob J Hyndman and George Athanasopoulos)

OLS combination


\[ y_t = {\alpha} + \sum_{i = 1}^P {\beta_i} f_{i,t} +\varepsilon_t.\]

The combined forecast is then given by:

\[f^{comb} = \widehat{\alpha} + \sum_{i = 1}^P \widehat{\beta}_i f_i.\]

Simple combination

Does not outperform the best model:

Train Test
arima 1.24 0.99
ets 1.17 0.87
nnet 1.27 0.98
dampedt 1.18 0.92
dotm 1.04 0.77 

# Simple Average
SA <- comb_SA(input_data) 
as.data.frame(names(SA))
>        names(SA)
> 1         Method
> 2         Models
> 3        Weights
> 4         Fitted
> 5 Accuracy_Train
> 6 Forecasts_Test
> 7  Accuracy_Test
> 8     Input_Data
formatC(SA$Accuracy_Test[,"RMSE"]/1000)
> [1] "0.7823"

OLS combination

Indeed outperform the best model:

Train Test
arima 1.24 0.99
ets 1.17 0.87
nnet 1.27 0.98
dampedt 1.18 0.92
dotm 1.04 0.77 

# OLS combination
OLSA <- comb_OLS(input_data) 
formatC(OLSA$Accuracy_Test[,"RMSE"]/1000)
> [1] "0.6715"

OLS Weights

A linear combination of couple of models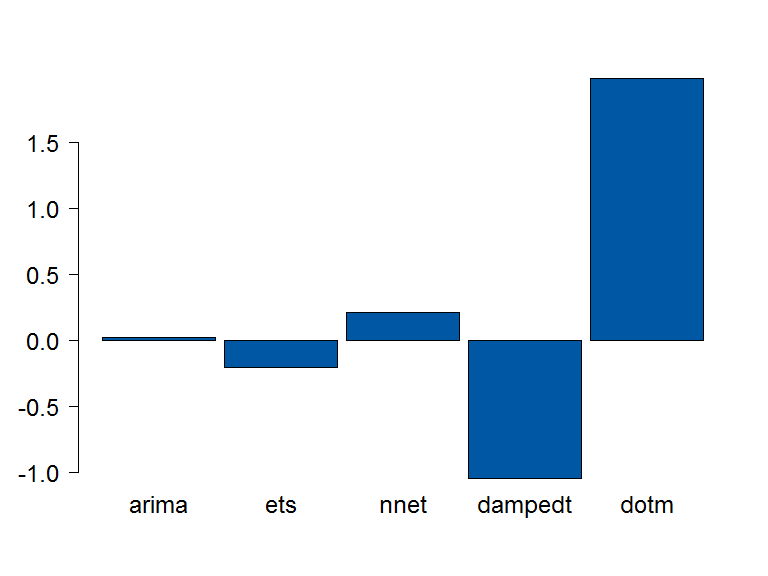

How come it works?

What can the ForecastComb package do for you?

What can the ForecastComb package do for you? (cont’d)

Part 2
Other things combination

Many widely used statistical techniques implicitly use forecast combination

  • Bagging
  • Random Forest
  • Moving average

    \[ D_t = (1-\lambda) \sum_{t=1}^ \infty \lambda^{t-1} (\varepsilon_{t-1}\varepsilon^ \prime_{t-1}) = (1-\lambda)(\varepsilon_{t}\varepsilon^ \prime_{t})+\lambda D_{t-1} \]

  • Shrinkage

    \[ \Sigma_{Combined}= \alpha \Sigma_{1} + (1-\alpha) \Sigma_{2} \]

  • Inception blocks in ConNN

For time series

For densities/probability

Even more

Simplicity makes me happy (Alicia Keys)

Part 3
A package is born

With an email

Email From Chris …

Partners in crime

Chris E Weiss

Chris

Gernot Roetzer

Gernot

Yours truly

Eran

Yet we have yet to meet

Collaboration and hard work

Work in progress

R journal Submission

Questions?

Thank you!

Eran Raviv
var RevealMath = window.RevealMath || (function(){ var options = Reveal.getConfig().math || {}; options.mathjax = options.mathjax || 'https://cdn.mathjax.org/mathjax/latest/MathJax.js'; options.config = options.config || 'TeX-AMS_HTML-full'; loadScript( options.mathjax + '?config=' + options.config, function() { MathJax.Hub.Config({ messageStyle: 'none', tex2jax: { inlineMath: [['$','$'],['\\(','\\)']] , skipTags: ['script','noscript','style','textarea','pre'] }, skipStartupTypeset: true }); MathJax.Hub.Queue( [ 'Typeset', MathJax.Hub ] ); MathJax.Hub.Queue( Reveal.layout ); // Reprocess equations in slides when they turn visible Reveal.addEventListener( 'slidechanged', function( event ) { MathJax.Hub.Queue( [ 'Typeset', MathJax.Hub, event.currentSlide ] ); } ); } ); function loadScript( url, callback ) { var head = document.querySelector( 'head' ); var script = document.createElement( 'script' ); script.type = 'text/javascript'; script.src = url; var finish = function() { if( typeof callback === 'function' ) { callback.call(); callback = null; } } script.onload = finish; script.onreadystatechange = function() { if ( this.readyState === 'loaded' ) { finish(); } } head.appendChild( script ); } })();