Toulo-useR!

Eran Raviv

July 11, 2019

Three parts to this talk

  1. On the ForecastComb package
  2. Other things combinations
  3. How the ForecastComb came to be

Part 1
The ForecastComb package

Forecast Combinations in our Context

  • What is it: \(f^{combined} = \frac{\sum_{i = 1}^P f_i }{P}\)
  • Why is it: Because it works
  • And why is that: More research is needed
  • Intuition: Biases and Model risk

An example

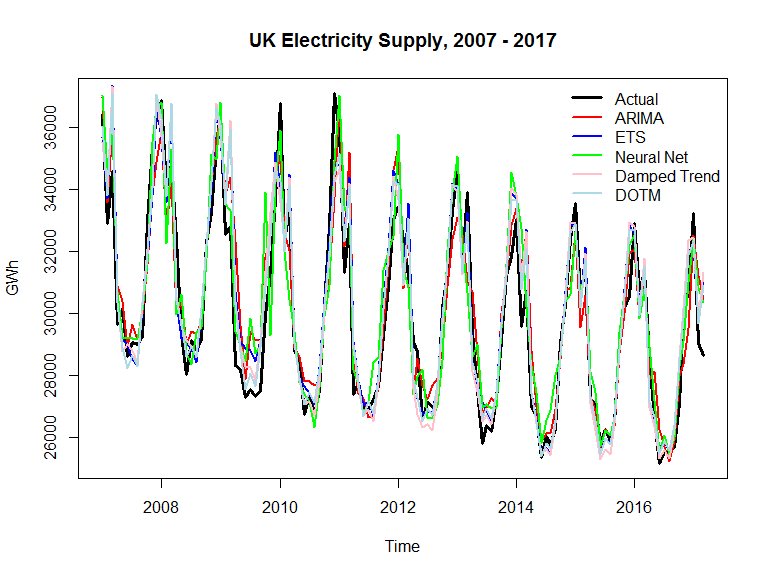
Data preparation

Individual performance

Train Test
arima 1.24 0.99
ets 1.17 0.87
nnet 1.27 0.98
dampedt 1.18 0.92
dotm 1.04 0.77

“…combining multiple forecasts leads to increased forecast accuracy. In many cases one can make dramatic performance improvements by simply averaging the forecasts.” (source: Forecasting: Principles and Practice. Rob J Hyndman and George Athanasopoulos)

OLS combination


\[ y_t = {\alpha} + \sum_{i = 1}^P {\beta_i} f_{i,t} +\varepsilon_t.\]

The combined forecast is then given by:

\[f^{comb} = \widehat{\alpha} + \sum_{i = 1}^P \widehat{\beta}_i f_i.\]

Simple combination

Does not outperform the best model:

Train Test
arima 1.24 0.99
ets 1.17 0.87
nnet 1.27 0.98
dampedt 1.18 0.92
dotm 1.04 0.77 

>        names(SA)
> 1         Method
> 2         Models
> 3         Fitted
> 4 Accuracy_Train
> 5     Input_Data
> 6        Weights
> 7 Forecasts_Test
> 8  Accuracy_Test
> [1] "0.7823"

OLS combination

Indeed outperforms the best model:

Train Test
arima 1.24 0.99
ets 1.17 0.87
nnet 1.27 0.98
dampedt 1.18 0.92
dotm 1.04 0.77 

> [1] "0.6715"

OLS Weights

A linear combination of couple of models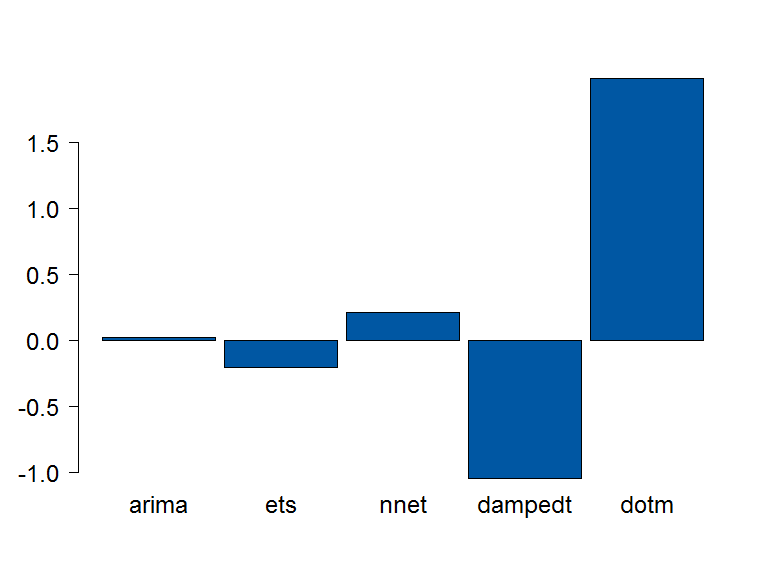

How come it works?

Let's look at some data:

What can the ForecastComb package do for you?

What can the ForecastComb package do for you? (cont’d)

Part 2
Other things combination

Many widely used statistical techniques implicitly use forecast combination

  • Bagging
  • Random Forest
  • Moving average

    $$ D_t = (1-\lambda) \sum_{t=1}^ \infty \lambda^{t-1} (\varepsilon_{t-1}\varepsilon^ \prime_{t-1}) = (1-\lambda)(\varepsilon_{t}\varepsilon^ \prime_{t})+\lambda D_{t-1} $$

  • Shrinkage

    $$ \Sigma_{Combined}= \alpha \Sigma_{1} + (1-\alpha) \Sigma_{2} $$

  • Inception blocks in ConNN

For time series

For densities/probability

Even more

Simplicity makes me happy (Alicia Keys)

Still more coming..

Not sure how much more mileage out of this

Part 3
A package is born

PPT at work

Quant round table

Code and manual

Then an email

Email From Chris …

Partners in crime

Chris E Weiss

Chris

Gernot Roetzer

Gernot

Yours truly

Eran

Yet we have yet to meet

Collaboration and hard work

Finally..

R journal Submission

R journal Ranking

Thank you!

Eran Raviv
var RevealMath = window.RevealMath || (function(){ var options = Reveal.getConfig().math || {}; options.mathjax = options.mathjax || 'https://cdn.mathjax.org/mathjax/latest/MathJax.js'; options.config = options.config || 'TeX-AMS_HTML-full'; loadScript( options.mathjax + '?config=' + options.config, function() { MathJax.Hub.Config({ messageStyle: 'none', tex2jax: { inlineMath: [['$','$'],['\\(','\\)']] , skipTags: ['script','noscript','style','textarea','pre'] }, skipStartupTypeset: true }); MathJax.Hub.Queue( [ 'Typeset', MathJax.Hub ] ); MathJax.Hub.Queue( Reveal.layout ); // Reprocess equations in slides when they turn visible Reveal.addEventListener( 'slidechanged', function( event ) { MathJax.Hub.Queue( [ 'Typeset', MathJax.Hub, event.currentSlide ] ); } ); } ); function loadScript( url, callback ) { var head = document.querySelector( 'head' ); var script = document.createElement( 'script' ); script.type = 'text/javascript'; script.src = url; var finish = function() { if( typeof callback === 'function' ) { callback.call(); callback = null; } } script.onload = finish; script.onreadystatechange = function() { if ( this.readyState === 'loaded' ) { finish(); } } head.appendChild( script ); } })();