R vs MATLAB - round 4

Machine estimated reading time:  [est_time]  

This is another comparison between R and MATLAB (Python also in the mix this time). In previous rounds we discussed the differences in 3d visualization, differences in syntax and input-output differences. Today is about computational speed.

Spoiler alert: MATLAB wins by a knockout.

A genuinely fair speed comparison across different software can be tricky. Almost all operations can be coded in more than one way. For example you can write your own mean function as sum(x)/length(x) or you can use an existing built-in mean function. Then, when measuring the computational speed we need to be sure measurement is completely separated from the actual computation. Your weight should not change when you step on the scales so to speak. Finally, we need an accurate estimate. So not rounded in any meaningful way, and sufficient repetition so that results can be trusted.

Which operations shall we measure? I chose two fairly common operations: random sampling from a normal distribution, and computing the mean of that vector using a built-in mean function. Repeating this 1000 times. We also vary the length of the vector. We perform the exercise once with a vector of size 10,000 and once with a vector of size 100,000. As simple implementation as possible in all three languages. The code is below.

Here are the results, multiplied by 1000 for readability, so 1 translates to 1/1000 seconds.

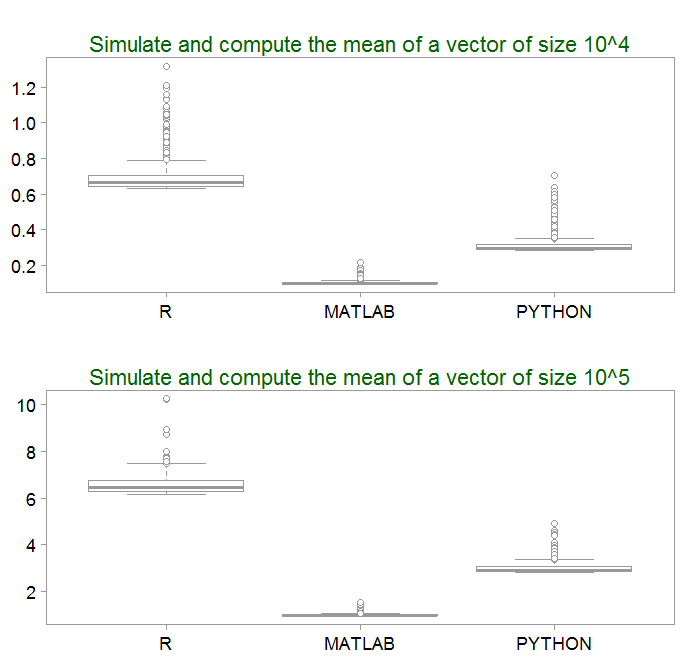
It’s a bird…It’s a plane…It’s MATLAB. Impressively fast, with extremely low variability, about 6 times faster than R and about 3 times faster than Python.
What we also notice is the asymmetry in the distribution of computational time. It may be something to do with the draws from the normal distribution (extreme draws slowed down computation maybe).
The computational time scales linearly with the size of the vector being drawn. As expected.

Few more comments:

The two operations: (1) drawing from a normal distribution and (2) computation of the mean are bundled together. Results may be somewhat different when it comes to only sampling, or only basic operations. I simply chose two common tasks which are often performed jointly (or variants thereof).
This is a vanilla implementation. Code can be faster in all three languages by using parallel computing or sending the code to another compiler. This is not considered here.
Ranking-wise, I could just as well have believed what is written table 1.1 in the machine trading book, (reviewed here.)

Still nice to get a feel for the magnitude.

Code:


import numpy as np
import time

mu, sigma = 0, 1 # mean and standard deviation
TT = 1000
pp= [10000, 100000]
py_timee= np.full((TT, 2), np.nan) 
for j in range(2):
    print(j)
    for i in range(TT):
        start_time = time.clock()
        s = np.random.normal(mu, sigma, pp[ j] )
        np.mean(s)
        py_timee[ [i], [j] ]  =  time.clock() - start_time

import numpy as np

import time

mu, sigma = 0, 1 # mean and standard deviation

TT = 1000

pp= [10000, 100000]

py_timee= np.full((TT, 2), np.nan)

for j in range(2):

print(j)

for i in range(TT):

start_time = time.clock()

s = np.random.normal(mu, sigma, pp[ j] )

np.mean(s)

py_timee[ [i], [j] ] = time.clock() - start_time


TT = 1000
p = [10000, 100000] 
matlab_timee= zeros(TT,2)
 for j = 1:2
 for i = 1:TT 
tic
x1 = randn(1,  p(j) ) ;
mean(x1) ; 
matlab_timee(i,j) = toc ;
end
j
end

TT = 1000

p = [10000, 100000]

matlab_timee= zeros(TT,2)

for j = 1:2

for i = 1:TT

tic

x1 = randn(1, p(j) ) ;

mean(x1) ;

matlab_timee(i,j) = toc ;

end


library(microbenchmark)
pp <- c(10^4, 10^5)
TT <- 1000
R_time <- matrix(nrow= TT, ncol= 2)
for (j in 1:2) {
for ( i  in 1:TT) {
R_time[i, j]= sum( microbenchmark( 
x1 <- rnorm(pp[j]),  mean(x1), 
times = 1)$time)
}}