silent evidence fallacy

I am talking here about money managers. for those of us who have one. We assume they understand about markets in such a way that they can, and will generate at least the benchmark returns, what ever this benchmark may be. Every once in a while you hear about a hedge fund, or an investor with astronomical abnormal performance. In the a book called “The Black Swan” (I thought it was boring by the way) Nasim Taleb talks about the Fallacy of Silent Evidence. That is, we hear about the oracle that managed to predict the 2008 crisis yet we do not really hear about those “oracles” that constantly predict the OIL prices to reach 400, since they did not reach 400. With so many opinions and players out there, someone is bound to outperform just because there are so many opinions and players out there. In econometrics there are ways to deal with it. Not to bore you, the curious reader can have a look here: FALSE DISCOVERY RATE, and can also google “A Reality Check for Data Snooping” or “A Test for Superior Predictive Ability”.

As an illustration, have a look at the following graph:

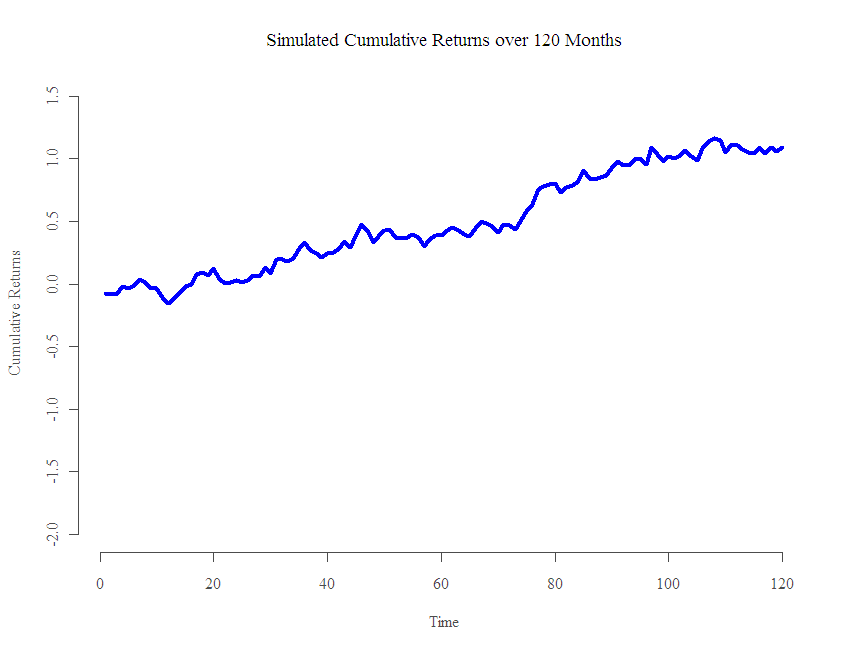Not bad it seems. Around 10% per year over 10 years… What I show is that this allegedly solid performance is simulated from the same distribution as all the others, and to better clarify my point, the distribution is a one that loses money over time. That is, the mean of the distribution is negative! (for non-statisticians this means the fund is on average losing money each month). I simulate 100 hedge funds monthly returns over 10 years time. I used the normal distribution with a standard deviation equals to the market monthly standard deviation and mean which is minus twice the mean of the market. So that if the market average monthly return is 0.5% then the mean of the distribution is -1%. (I use the SNP 500 return as proxy for the market). So you see, this figures comes from the same poor distribution as all the others, the only reason it looks nice is because I generated 100 of those and hand picked one that seems to outperform.

Don’t get me wrong, I am sure reading “financial times” and “Wall Street Journal”, watching CNBC and following the market sharpens your understanding and analytical skills, but beating Mr. market is tough, both timing and stock selection. My point is that there is no reason to be impressed by those magical money machines you read or hear about. And now for the big picture:

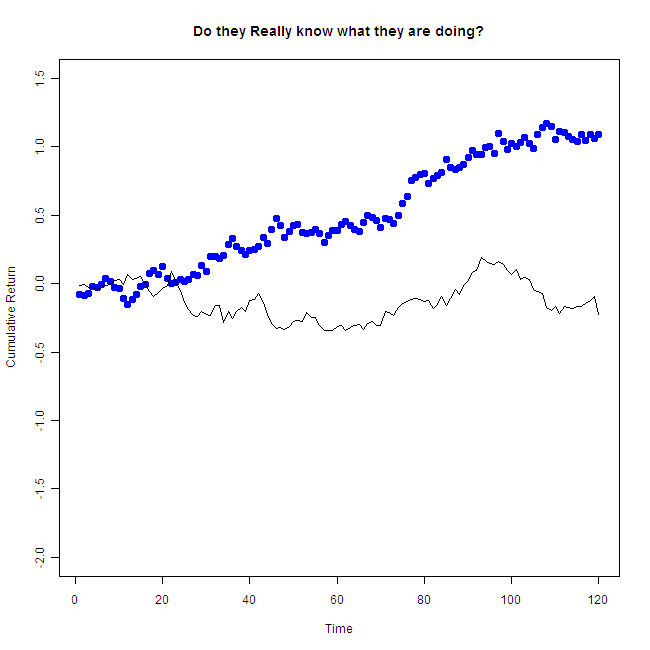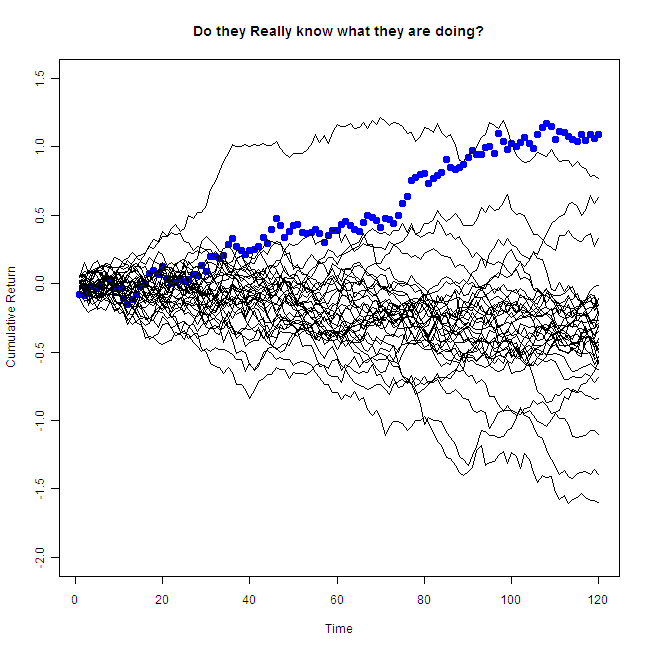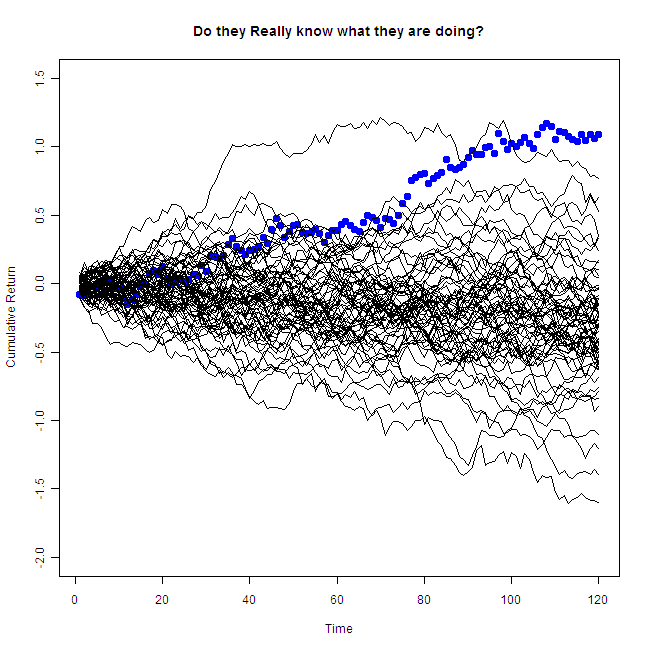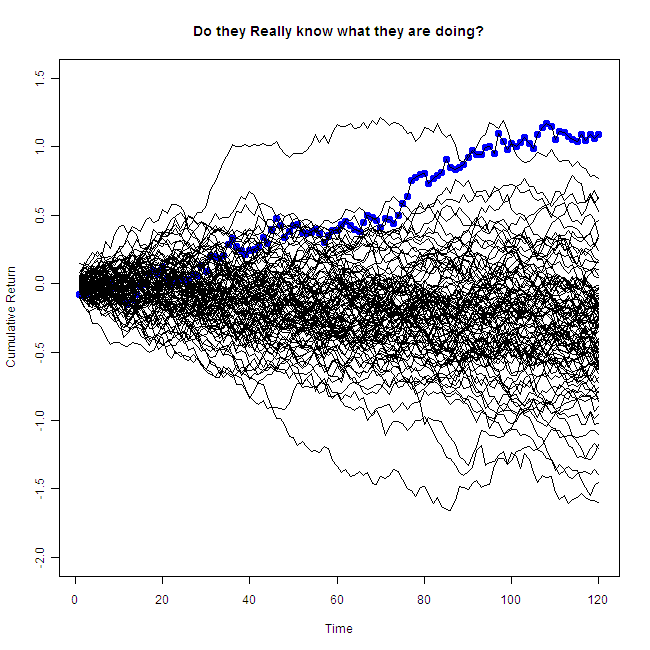That is the same performer, but now you can see the other draws as well. So.. “Do they really know what they are doing?”, without accounting for all other players, we have no idea. Don’t fall of your chair next time you are face to face with an “oracle”.

As always, the code is below. Thanks for reading.


library(quantmod)
library(PerformanceAnalytics)
start<-format(as.Date("2001-11-19"),"%Y-%m-%d") # the start date of tna
end<- format(Sys.Date(),"%Y-%m-%d") # yyyy-mm-dd
dat1 = as.matrix((getSymbols("SPY", src="yahoo", from=start, to=end, auto.assign = FALSE)))
dim(dat1)
sdmarket = sd(periodReturn(dat1, period = 'monthly')) # 0.05629304
meanmarket = mean(periodReturn(dat1, period = 'monthly')) # 0.01280399
n = 120 # 10 years
l = 100 # assume 100 is the number of hedge funds
bench = cumsum(rep(.5,n)) 
bench2 = cumsum(rnorm(n,meanmarket,sdmarket)) 
perf = matrix(nrow = l, ncol = n) ; perf2 = matrix(nrow = l, ncol = n)
maxperfbin = NULL ; maxperfnorm = NULL
for (i in 1:l){
perf[i,] = cumsum(rbinom(n,1,.45))
perf2[i,] = cumsum(rnorm(n,-2*meanmarket,sdmarket)) # these guys generate negative twice the return of SNP
maxperfbin[i] = perf[which.max(perf[,n]),n]/bench[n] - 1
maxperfnorm[i] = perf2[which.max(perf2[,n]),n]/bench2[n] - 1
}
par(mfrow = c(2,1))
plot(bench, ty = "l", col = 2, lwd = 4, ylim = c(0,75))
for (i in 1:l){
lines(perf[i,])
}
lines(perf[which.max(perf[,n]),], col = 4, lwd = 4)
plot(bench2,, ty = "l", ylim = c(-2,1.5), col = 2, lwd = 4) 
for (i in 1:l){
lines(perf2[i,])
}
lines(perf2[which.max(perf2[,n]),], col = 4, lwd = 4)

plot(perf2[which.max(perf2[,n]),], ty= "l",col = 4, lwd = 4, xlab = "Time", ylab = "", ylim = c(-2,1.5), 
     main = "Simulated Cumulative Returns over 120 Months")