Is bitcoin a bubble? I don’t know. What defines a bubble? The price should drastically overestimate the underlying fundamentals. I simply don’t know much about blockchain to have an opinion there. A related characteristic is a run-away price. Going up fast just because it is going up fast.
How fast the price of bitcoin moves up? In order to quantify this we can design a short exercise testing how large the exponent of the price movement. Easy enough. We download bitcoin prices, fit a polynomial regression of the order 1 through 10. And check the information criteria to get a feeling for the fit, is polynomial of the six degree much better than that of two? Here is the resulting chart followed by an information criteria table.
Bitcoin dollar price (divided by 1000 for readability)
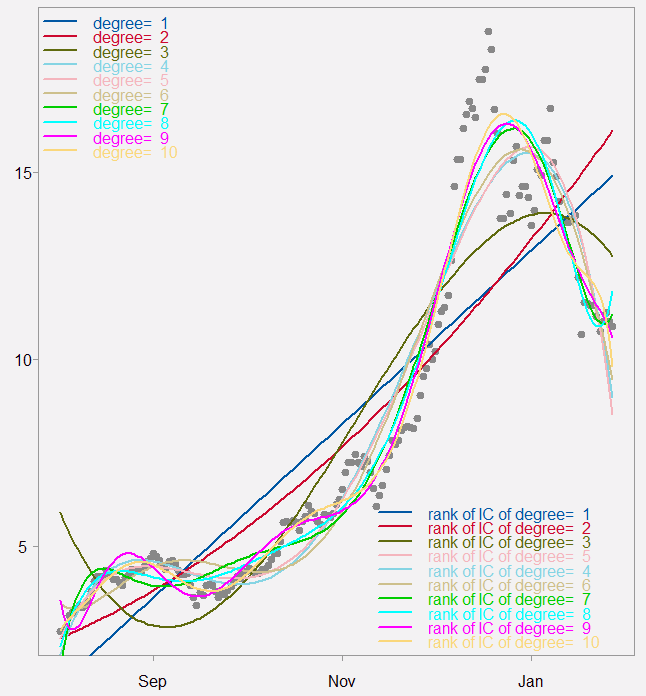
Top left legend shows those regression curves fitted, but the bottom right shows the ranking based on the Akaike Information Criteria.
Information criteria for the different polynomial fit
| AIC | BIC | |
|---|---|---|
| Degree= 1 | 3.26 | 3.27 |
| Degree= 2 | 3.10 | 3.12 |
| Degree= 3 | 2.92 | 2.94 |
| Degree= 4 | 2.79 | 2.81 |
| Degree= 5 | 2.79 | 2.82 |
| Degree= 6 | 2.77 | 2.80 |
| Degree= 7 | 2.78 | 2.80 |
| Degree= 8 | 2.66 | 2.69 |
| Degree= 9 | 2.60 | 2.63 |
| Degree= 10 | 2.60 | 2.64 |
Looking at the table it is so that the IC’s point to a very large exponent (9 or 10 is the minimum). However, over the four degree there is very little drop in the value of the IC’s. If asked, a four degree polynomial is adequately parsimonious at this point in time.
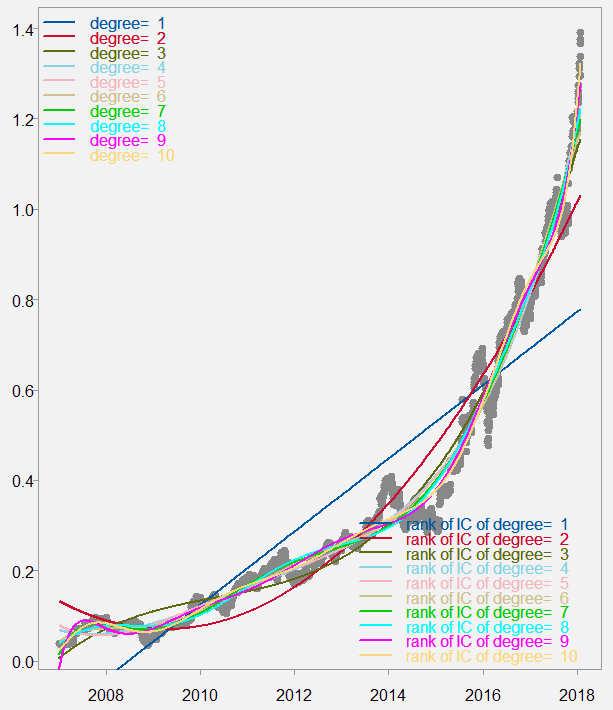
Admittedly, if you perform the same exercise a month ago results would markedly differ. Meaning it is quite time-sensitive. That said, if you perform the same exercise on Amazon stock price, it does look abnormally fast sloping (see figure below). But there it can be argued that the price does not stray much from fundamentals, Amazon’s barrel is probably full of bullets yet to be fired.
The main takeaway here is not so much bitcoin related. But the simple exercise and code to help you quantify how exponential is exponential growth.
Amazon dollar price (divided by 1000 for readability)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
library(quantmod) ; citation("quantmod") bitcoin <- getFX('BTC/USD', auto.assign = F, ,src='google') degreee <- 10 ply_expansion <- polym(seq(x), degree = degreee, raw = TRUE) # polynomial expansion plot(x/1000 ~ index(bitcoin), ylab="") bic <- aic <- rep(NA, degreee) for (i in 1:degreee){ lm0 <- lm(x~ ply_expansion[,1:i]) aic[i] <- AIC(lm0) bic[i] <- BIC(lm0) lines(lm0$fit/1000 ~ index(bitcoin), col= coll[i], lwd=2) } |









One comment on “Bitcoin exponential growth”