Matlab has it this time, with solid 3D plotting capabilities.
Category: R
Comments on Comments in R
When you are busy with a lengthy project, like writing a paper, you create many objects along the way. Every time you log into the project, you need to remember what is what. In the past, each new working session I used to rerun the script anew and follow what each line is doing until I get back the objects I need and continue working. Apart from helping you remember what you are doing, it is very useful for reproducibility, at least given your data, in the sense that you are sure nothing is overrun using the console and it is all there. Those days are over.
Understanding Multicollinearity
Roughly speaking, Multicollinearity occurs when two or more regressors are highly correlated. As with heteroskedasticity, students often know what does it mean, how to detect it and are taught how to cope with it, but not why is it so. From Wikipedia: “In this situation (Multicollinearity) the coefficient estimates may change erratically in response to small changes in the model or the data.” The Wikipedia entry continues to discuss detection, implications and remedies. Here I try to provide the intuition.
How Important is Variable Selection?
Very.
If you have 10 possible independent regressors, and none of which matter, you have a good chance to find at least one is important.
Quantify your jogging
Numbers are useful (I think we can all agree on that..). If you own a smart phone, you can install this runmeter app. When you run, you can take the smartphone with you and activate this app to collect interesting numbers like distance, pace, fastest pace, heart rate*, calories etc. Now we can load the statistics collected over the past months into R and have a quantified look at the progress.
R and Dropbox
When you woRk, you probably have a set of useful functions/packages you constantly use. For example, I often use the excellent quantmod package, and the nice multi.sapply function. You want your tools loaded when R session fires.
Moving Average Representation of VAR
A vector autoregression (VAR) process can be represented in a couple of ways. The usual form is as follows:
Quantile Autoregression in R
In the past, I wrote about robust regression. This is an important tool which handles outliers in the data. Roger Koenker is a substantial contributor in this area. His website is full of useful information and code so visit when you have time for it. The paper which drew my attention is “Quantile Autoregression” found under his research tab, it is a significant extension to the time series domain. Here you will find short demonstration for stuff you can do with quantile autoregression in R.
On p-value
Albert Schweitzer said: “Example is not the main thing in influencing others. It is the only thing.”, so I start with it.
Live Correlation plot, shiny improvement.
Open CPU is a great project. Few months back, I wrote a function for plotting a moving window of the market average correlation. Jeroen C.L. Ooms was nice enough to upload it to their server. Something is now changed. Quotes now return as a character class, as oppose to numeric. This messes up the function and the plot does not renders. I don’t wish to disturb Jeroen C.L. Ooms again with the correction for the code (despite his kind replies in the past). This problem creates the opportunity to look at the glistening “Shiny” package. I used it to (quickly..) build an app for the plot. You can now view a live correlation plot with the moving window of your choice. Live, as the app requests current market data. The width of the window for correlation calculation is given as an input parameter.
A Simple Model for Realized Volatility
The post has two goals:
(1) Explain how to forecast volatility using a simple Heterogeneous Auto-Regressive (HAR) model. (Corsi, 2002)
(2) Check if higher moments like Skewness and Kurtosis add forecast value to this model.
On Volatility Proxy
Volatility is unobserved. Hence we need to use observed quantity as a proxy. Every once in a while I still see people using squared daily return as a proxy. However, there is ample evidence that it is a bad one. Bad in a sense that it is noisy, which means that although on average it is a good estimate, on any individual day the estimate can be very far from the actual unobserved volatility. Here is a figure of the alleged standard deviation in the form of (square root of the) squared daily return for the recent year:
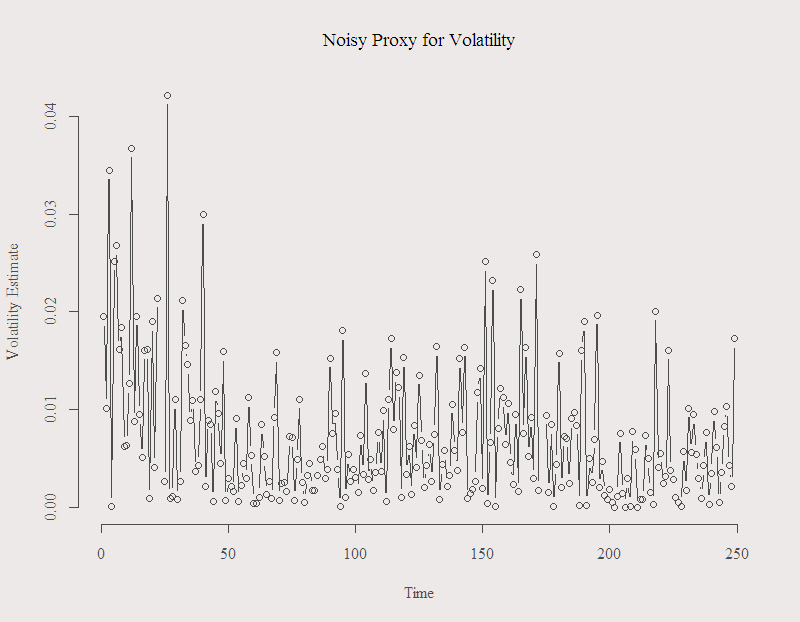 You can see that in many days, this noisy estimate suggests that the volatility was around 2% and more. To me, it does not make too much sense. The series is the S&P 500, so a move of 3% is a BIG one. You can also see how “jumpy” the series is. The figure illustrates why we should avoid using this estimate.
You can see that in many days, this noisy estimate suggests that the volatility was around 2% and more. To me, it does not make too much sense. The series is the S&P 500, so a move of 3% is a BIG one. You can also see how “jumpy” the series is. The figure illustrates why we should avoid using this estimate.
Forecasting the Misery Index, follow-up
Five months ago I generated forecasts for the Eurozone Misery index. I used the built-in “FitAR” package in R. Using different models differing in their memory length (how many lags were considered for each model) 24 months ahead forecasts were generated. Might be interesting to see how accurate are the forecasts. The previous post is updated and few bugs corrected in the code. The updated data is public and can be found here. It is the sum of inflation rate and unemployment rate in the Euro-zone area.
Volatility forecast evaluation in R
In portfolio management, risk management and derivative pricing, volatility plays an important role. So important in fact that you can find more volatility models than you can handle (Wikipedia link). What follows is to check how well each model performs, in and out of sample. Here are three simple things you can do:
A shrinkage estimator for beta
In the post pairs trading issues one of the problems raised was the unstable estimates of the stock’s beta with respect to the market. Here is a suggestion for a possible solution, which is not really a solution but more stuff to do to make you feel less stupid when trading based on your fragile estimates.
