R tips and tricks – Timing and profiling code

Modern statistical methods use simulations; generating different scenarios and repeating those thousands of times over. Therefore, even trivial operations burden computational speed.

In the words of my favorite statistician Bradley Efron:

“There is some sort of law working here, whereby statistical methodology always expands to strain the current limits of computation.”

In addition to the need for faster computation, the richness of open-source ecosystem means that you often encounter different functions doing the same thing, sometimes even under the same name. This post explains how to measure the computational efficacy of a function so you know which one to use, with a couple of actual examples for reducing computational time.

First, use the package microbenchmark. It provides infrastructure to measure and compare the execution time of different R code. In Matlab you can use the the tic toc functions and in Python you can use the clock function from the time module. You can find some toy code here.

Example: you need to extract the first value of a vector. I grew up with the function head(vector, n= 1) which asks the first value of the vector. In Python’s Pandas it is vector.head(1). Now, there are other functions which, perhaps, are more speedy/efficient.

Google says that there is a function which is called first. Actually, a function called first is available from the dplyr package, the xts package and the data.table package. So we have 4 different functions (that I know of, probably more out there) that do the same thing. If speed is of the essence, which function you should use? which is fastest? The following code-snippet answers.

The triple colon operator ::: is used here to access functions within the package without attaching the actual package to the search path. Since the packages are not of the same size I use the triple colon operator but the use of the double colon operator, :: is better practice in general. Here are the results of the timing operation based on 1000 times of executing each one of those function. The y-axis is divided by 10000 for readability.

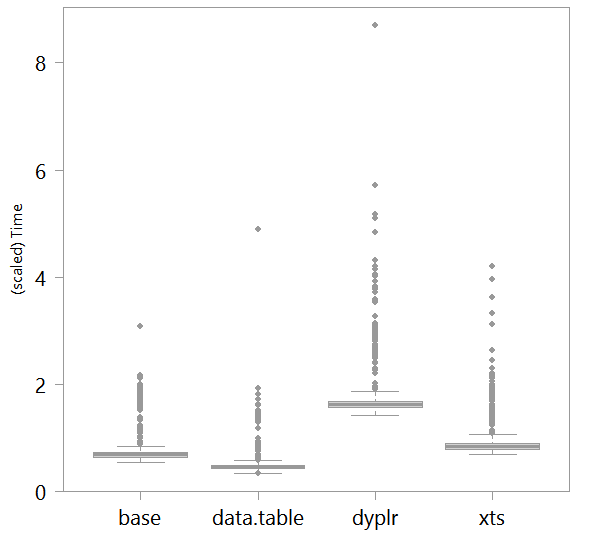
With the risk of over-generalization, based on this analysis/figure the recommendations are: (1) use data.table (as an aside, I hear a lot of other good things about it). (2) Do not use dplyr when speed is important. (3) In this example, if the function head is replaced by the function first from the data.table package you can save around 33% of computational time. If you are still reading this, I can imagine your code has many pockets where you can improve the speed, so time your code if you enjoy need it. Doing something like this within few pockets of your code could save appreciable time.

Speeding up eigenvalue decomposition

Eigenvalue decomposition is a mathematical operation which is common, and is computationally expensive even in fairly moderate dimension. The eigen function is the go-to. I found two more faster solutions. You can use the irlba function from the irlba package which is good for very large matrices, or the eigs_sym function from the RSpectra package, which take advantage for when you don’t need the whole vector of eigenvalues (as is often the case) by simply replying with the first few largest values, and conserve computational time as a result. The code below illustrates the speed gain.

expr	min	lq	mean	median	uq	max	neval
eigen	23.9	24.8	26.8	26.1	27.9	45.1	1000
eigs_sym	16.2	16.8	18.2	17.6	18.9	39.8	1000

So if you are interested in say the top few eigenvalues you can save good amount of time by using the eigs_sym function.

Optimize your code away, friends.

References

Efron, Bradley. “The bootstrap and modern statistics.” Journal of the American Statistical Association 95.452 (2000): 1293-1296.

Advanced R

Olaf Mersmann (2019). microbenchmark: Accurate Timing Functions. R package version 1.4-7.

Large-Scale Eigenvalue Decomposition and SVD with RSpectra