Why statistical bootstrap

I often write about bootstrap (here an example and here a critique). I refer to it here as one of the most consequential advances in modern statistics. When I wrote that last post I was searching the web for a simple explanation to quickly show how useful bootstrap is, without boring the reader with the underlying math. Since I was not content with anything I could find, I decided to write it up, so here we go.

Why do we need bootstrap?

Long ago, I was teaching students some introductory statistics. On their exam there would always be some story regarding the weight of airplane parts, or the volume of some soft drink. At the end of the very interesting story no doubt, students would be questioned whether the mean is significantly different from what is initially stated by the supplier or vendor. Essentially aiming to check if the student knows which statistical test should be used.

It was easy for students to remember the heuristic: “If the number of observation is larger than 30, then we use the z-test”.

And if not? I would ask, “then I use the t-test” (BZZZ, wrong answer).

For significance testing you need to know the distribution of your test-statistic. If we compute the average using more than 30 observations, then we know the distribution is (asymptotically) normal. But if we have less than that, say we have only 10 observations, it is only t-distributed if the individual variable is normally distributed. So not the average volume in those soft drink bottles, but the volume in each individually sampled bottle . If the original variable is normally distributed, then the average, even if computed using only a sample of 10, would be t-distributed. If it is not given in that exam question that the original variable is normally distributed, then t-test is an incorrect answer.

Now the student would ask: “and what if they don’t provide us with any more details on the distribution of the individual observations?” then I would reply that “there are ways, but you are not there yet”. The answer is of course to bootstrap. Basically, the bootstrap methodology is the alternative for the situation where you can’t, or you don’t want to rely on the asymptotic distribution.

Illustration

Let’s simulate some numbers and look at the distribution of an average in three cases: (1) when when it is based on 100 observations drawn from uniform distribution, (2) when it is computed using 10 draws only, uniformly distributed also, and (3) when it is computed using 10 observation only, but the original observations themselves are normally distributed. Coming back to that hypothetical conversation, the mean of (1) can be tested using z-test. The mean of (3) can be tested using t-test, and the mean of (2) was a ‘trick’ question, because you can’t use z-test nor t-test. Back then, Bootstrapping was taught only in a more advanced course (maybe by now it is different) so the student should reply she does not have sufficient details to apply any standard test.

Simulation:

The distribution of the average, for convenience I superimpose a perfect normal curve in blue:

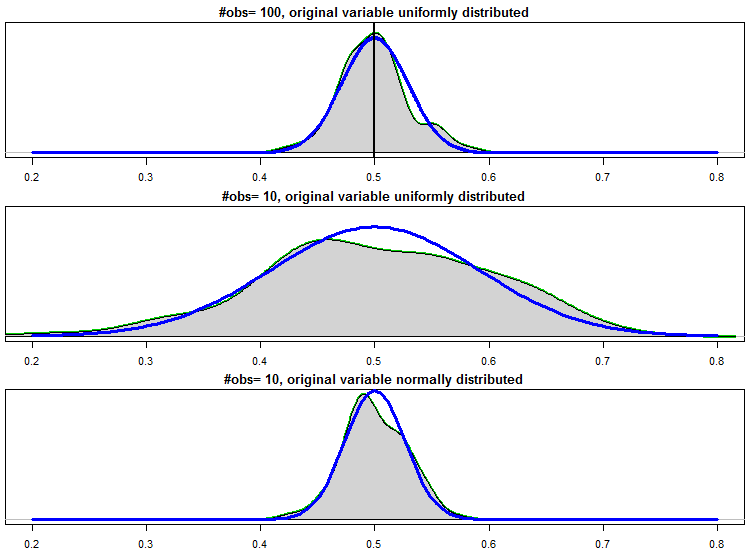
Few things we see here:

• The first is that we have a few kinks even when we have 100 observations. This tells you something about convergence and approximations. For a large enough number of observations the green and blue curve should fully overlap.
• The second is that when we have only 10 observation, even with nicely behaved symmetric distribution like uniform, convergence is simply not fast enough so that we can comfortably replace empirical with the asymptotic distribution. This is the key reason that we simply cannot rely on asymptotic. The distribution of the average is not uniform, since it is an average (rather a single observation- which IS uniform). The distribution of the average is not normal neither, since the number of observations is not large enough for the asymptotic approximation to ‘kick-in’.

If we denote mean_0 as the mean under the null hypothesis, the next figure shows the distribution of the test statistic, the usual (average – mean_0)/(standard error). Here we can focus not so much on the shape. We use the test statistic to decide whether to reject the null hypothesis or not. So I superimpose the traditional critical values (-1.96 and 1.96) in light blue. We know from the way we simulated that the mean is actually 0.5. What we care about now is how many “unlucky” scenarios we have whereby we have decided to reject the null (which we know is correct), i.e. the test statistics falls in the tails. For comparison, I also include a perfect normal curve, so that we can compare the behavior of the tails.

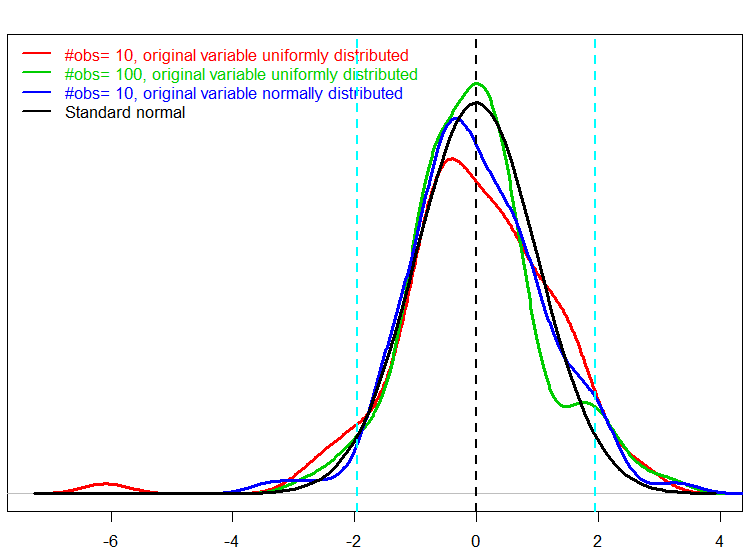
We can ignore the wiggling between the light blue dashed lines since we are only interested in the shape of the tails: whether we get the exact tail shape as that of the standard normal (in black). If that would be the case we could say we have correct coverage (that is the term we use to describe the ‘inner’ 95%).

From the figure it is clear that when using asymptotics, it is better to have just a few observation when the original variable is normally distributed, than having ten times as many observations when the original variable has a non-normal distribution; the green tails are fatter than that of normal, which will create more false rejections. Of course, the red line is completely off.

Takeaway from this is that when you rely on asymptotics, adding more observations can help, but a transformation of the original variable which would bring its shape closer to that of normal will likely to achieve better performance in terms of coverage. This also shows that asymptotic analysis based on moderate amount of data would benefit from a good portion of healthy skepticism.

We can compute and see, out of the 100, under the null (which we know is correct), how many wrongful rejections we have:

Recall the correct number based on asymptotics should be 0.05. This is simply to confirm what we observed in that figure. Even if we have only 10 observation, but that are normally distributed we get better coverage (closer to 5%) than when we have 10 times that amount, with a distribution which is not normal. This goes to show how the importance of having a lot of data, especially so when it comes to making some asymptotics-based inference.

Bootstrap

The aim it to show here is that bootstrapping accounts for the empirical distribution of the test statistic (which has the number of observation built into it..), so you get good coverage without relying on asymptotics.

We now treat each of the 100 simulated sequences as if it were the observed values. We bootstrap 500 samples for each of those 100 simulated series. This is in order to create the empirical distribution of the test statistic for each of the 100 series. Again, the aim is later to check what is the coverage we get when we look at a distribution of the test statistics which is bootstrapped based on the 500 samples, rather than assumed asymptotically.

We now have 3 objects of type array. Each of which have 500 simulated bootstrap samples, for each of the 100 of the initial simulated series, and each bootstrap sample is of the length of the original series from which we sample. So the object xfew_boot has dimension 10 ∗ 100 ∗ 500. Stay with me.

We now compute the test statistic based on the mean and standard error of the bootstrap distribution. Note that we should have 500 of those, for each of the 100 series.

What we do now is to check how many type one error we have, or how many false rejections. We don’t compare it not to the asymptotic critical values coming from the familiar tables (+1.96 and -1.96) but we compare our test statistics to the one we would expect to see under the null, given the empirical distribution. The way to do that is to scale the test statistics such that it is centered at zero. You see, the center is different since this is what we expect to see, given the empirical distribution and under the null. We created our own “t-table”-like, using the empirical distribution. Equipped with this new analogue, we use the empirical relevant quantiles as our relevant critical values. If our realization is in the extremes, far from those 0.975 and 0.025 quantiles it would mean that the center of what we observe is different from the center we would expect to see, accounting for the shape of the empirical distribution.

	Bootstrap	Asymptotic	Correct
many	0.053	0.1	0.05
few	0.055	0.1	0.05
fewnorm	0.053	0.05	0.05

You can see that the bootstrap-based testing has the correct coverage.

Think about the most tricky scenario for the asymptotic to handle: the one which has only few observations which are not normal. Look at the big difference in coverage. The reason for the bootstrap to have correct coverage even in that case is that we account for the shape of that distribution which again, has its non-normality and the small number of observations built into that shape.

With this, I hope you are persuaded. Of course, classical Fisherian statistic has its place. If we have a good knowledge of the underlying distribution, then bootstrapping is inferior. It is more complex, computationally more expensive and less accurate. But between us, how often those textbook distribution appear in real life problems?

Bootstrapping is a way in which we can relax asymptotic assumptions, because they are unrealistic, or because we simply don’t trust a speedy enough convergence.