How flexible neural networks really are?

Very!

A distinctive power of neural networks (neural nets from here on) is their ability to flex themselves in order to capture complex underlying data structure. This post shows that the expressive power of neural networks can be quite swiftly taken to the extreme, in a bad way.

What does it mean? A paper from 1989 (universal approximation theorem, reference below) shows that any reasonable function can be approximated arbitrarily well by fairly a shallow neural net.

Speaking freely, if one wants to abuse the data, to overfit it like there is no tomorrow, then neural nets is the way to go; with neural nets you can perfectly map your fitted values to any data shape. Let’s code an example and explain the meaning of this.

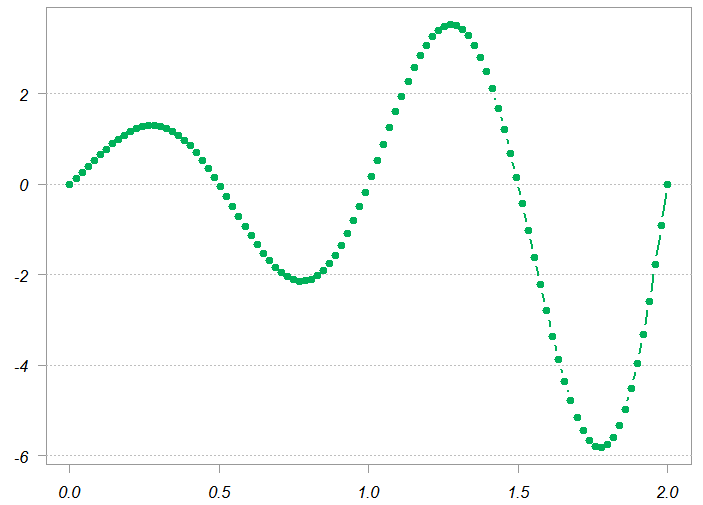
I use figure 4.7 from the book Neural Networks and Statistical Learning as the function to be approximated (as if the data comes from a noisy version of this curve below).


x <- seq(0, 2, length.out= 100)
fx <- function(x){ sin(2*pi*x) * exp(x) }
y <- fx(x)
plot(x,y)

x <- seq(0, 2, length.out= 100)

fx <- function(x){ sin(2*pi*x) * exp(x) }

y <- fx(x)

plot(x,y)

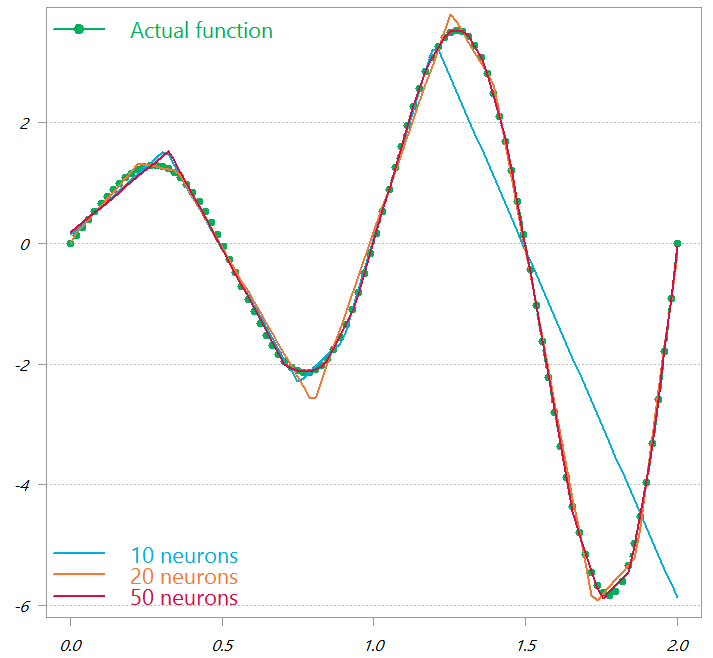
Using the code below, you can generate the function plotted by a linear combination of Relu-activated neurons. In a neural net those are the hidden units. I use 10, 20, and 50 neurons. You can see below that the more neurons you use the more flexible is the fit. With only 10 neurons, so-so, respectable fit with 20, and a wonderful fit with 50 (in red) which captures almost all turning points.

Nice, but what’s the point?

The point is that with great (expressive) power comes great (modelling) responsibility.

There is a stimulating paper by Leo Breiman (the father of the highly successful random forest algorithms) called “Statistical modeling: The two cultures”. Commenting on that paper my favorite statistician writes

“At first glance it looks like an argument against parsimony and scientific insight, and in favor of black boxes with lots of knobs to twiddle. At second glance it still looks that way…”

Reason and care are needed for developing trust around deep learning models.

Drink and model, both responsibly (tip: sometimes better results if you do both simultaneously).

Appendix

Code for the approximation


relu <- function(z) ifelse(z >= 0, z, 0)

approx_fun <- function(x, a = a, b = b, c = c, d = d) {
  tmpp <- matrix(nrow = length(x), ncol = num_funs)
  for (j in 1:num_funs) {
    for (i in 1:length(x)) {
      tmpp[i, j] <- b[j] * relu(c[j] + d[j] * x[i])
    }
  }
  a + apply(tmpp, 1, sum)
}


relu_approx <- function( par ) {
  a <- par[1]
  c <- par[2:(num_funs+1)]
  b <- par[(num_funs+2):(2*num_funs+1)]
  d <- par[(2*num_funs+2):(3*num_funs+1)]
approx <- approx_fun(x, a= a, c= c, b= b, d= d )
er <- (approx - fx(x))^2
er <- sum(er)
return(er)
}

num_funss <- c(10, 20, 50)
 approx_x_cache <- list()
for (i in num_funss) {
  num_funs <- i
  op1 <- optim(
  par = rnorm(i * 3 + 1),
  fn = relu_approx,
  method = "BFGS",
  control = list(trace = 1, maxit = 1000) 
  )

approx_x <- approx_fun(x,
    a = op1$par[1],
    b = op1$par[(i + 2):(2 * i + 1)],
    c = op1$par[2:(i + 1)],
    d = op1$par[(2 * i + 2):(3 * i + 1)]
  )
approx_x_cache[[i]] <- approx_x
}

relu <- function(z) ifelse(z >= 0, z, 0)

approx_fun <- function(x, a = a, b = b, c = c, d = d) {

tmpp <- matrix(nrow = length(x), ncol = num_funs)

for (j in 1:num_funs) {

for (i in 1:length(x)) {

tmpp[i, j] <- b[j] * relu(c[j] + d[j] * x[i])

}

a + apply(tmpp, 1, sum)

}

relu_approx <- function( par ) {

a <- par[1]

c <- par[2:(num_funs+1)]

b <- par[(num_funs+2):(2*num_funs+1)]

d <- par[(2*num_funs+2):(3*num_funs+1)]

approx <- approx_fun(x, a= a, c= c, b= b, d= d )

er <- (approx - fx(x))^2

er <- sum(er)

return(er)

}

num_funss <- c(10, 20, 50)

approx_x_cache <- list()

for (i in num_funss) {

num_funs <- i

op1 <- optim(

par = rnorm(i * 3 + 1),

fn = relu_approx,

method = "BFGS",

control = list(trace = 1, maxit = 1000)

)

approx_x <- approx_fun(x,

a = op1$par[1],

b = op1$par[(i + 2):(2 * i + 1)],

c = op1$par[2:(i + 1)],

d = op1$par[(2 * i + 2):(3 * i + 1)]

)

approx_x_cache[[i]] <- approx_x

}

Encore for the interested geek – link with polynomial regression

In 1961 it was shown (Weierstrass approximation theorem) that any well behaved function could be, as above, approximated arbitrarily well by a polynomial function. In that regards “..fitting NNs actually mimics Polynomial Regression, with higher and higher-degree polynomials emerging from each successive layer..” (quoted from the third reference below).

Universal approximation theorem

Let $F$ be a continuous function on a bounded subset of $D$ -dimensional space. Then there exists a two-layer neural network $\wh{F}$ with finite number of hidden units that approximate $F$ arbitrarily well. Namely, for all $x$ in the domain of $F$ ,

$\; \vert \vert F(x) - \widehat{F}(x)\vert \vert < \varepsilon.$

References

Hornik, K., et al.Multilayer feedforward networks are universal approximators. Neural Networks 2, 5 (1989), 359 – 366

Breiman, Leo. “Statistical modeling: The two cultures (with comments and a rejoinder by the author).” Statistical science 16, no. 3 (2001):
199-231.

Cheng, Xi, Bohdan Khomtchouk, Norman Matloff, and Pete Mohanty. “Polynomial regression as an alternative to neural nets.” arXiv preprint arXiv:1806.06850 (2018).

Katznelso., Y., and Rudin, W. The stone-weierstrass property in banach algebras.Pacific Journal of Mathematics 11, 1 (1961), 253–265.

You might also like:

One comment on “How flexible neural networks really are?”

Michael Scharrer says:

05/07/2021 at 6:20 PM

Great explanation.
I wonder what happens when you push the number of neurons much higher. Polynomial interpolation starts to degrade rapidly once the order gets close to the number of data points. Does something similar happen in this model?