Every form of strength is also a form of weakness*. I love statistics, but I focus to much on methodology, which is not for everyone. Some people (right or wrong) question: “wonderful sir, but what can I do with it?”.
A new paper titled “Beta in the tails” is a showcase application for why we should focus on correlation structure rather than on average correlation. They discuss the question: Do hedge funds hedge? The reply: No, they don’t!
The paper “Beta in the tails” was published in the Journal of Econometrics but you can find a link to a working paper version below. We start with a figure replicated from the paper, go through the meaning and interpretation of it, and explain the methods used thereafter.
Main point
Hedge funds don’t hedge.
Credit Suisse Hedge Fund Index betas computed on sorted market monthly returns (as measured by the returns on the SPY ETF).
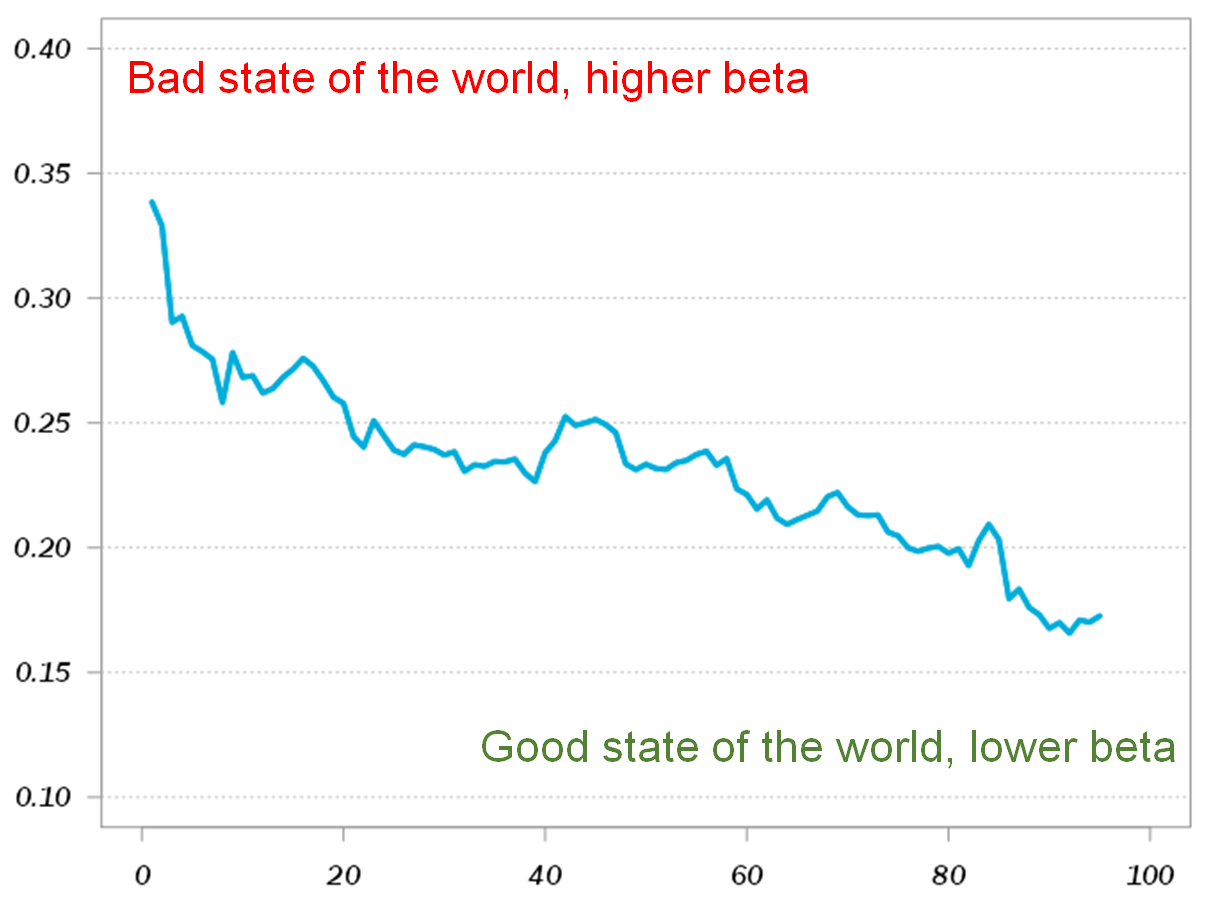
rq function from the quantreg package. On the X-axis: the actual quantiles (e.g. 50 means roughly median monthly returns).
The data used is taken from lab.credit-suisse.com (registration needed). The figure shows that when market returns are low (lower quantiles on the X-axis), the hedge fund’s returns move more in tandem (so also low), then when market returns higher end (higher quantiles on the X-axis). If hedge fund are actually serving us as a hedge, we should have seen exactly the reverse. When markets do poorly for the individual, the hedge fund returns would “kick in” to compensate for market losses.
More interesting points from the paper:
- The figure above is typical, and holds true for almost all hedge fund styles. The wording “in the tails” is because the slope is very steep when returns are at the very low quantiles (left tail of the return distribution). Meaning the hedge, if that is what you tell yourself you are doing, fails exactly when you need it the most, so add-on tail risk.
- Two styles are actually not a bad hedge: managed futures and equity market neutral. It’s nice to see an analysis I have made back in 2012 about most profitable hedge fund style actually holds up, as 2 out of the 3 winning styles are indeed market neutral.
Methodology
I followed a paper written by Dirk Baur: The structure and degree of dependence: A quantile regression approach, and used a slightly revised code from the post Correlation and correlation structure (1); quantile regression. Basically you create a quantile regression loop through the different quantiles to estimate the beta. While we can discuss the more general notion of correlation, clearly hedge funds follow the market rather than the other way around, so we can simply look at the beta from that regression. The actual function I used is given below.
References
Relevant code
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
library(quantreg) corquantile <- function(seriesa,seriesb,k=10){ if(length(seriesa)!=length(seriesb)){stop("length(seriesa)!=length(seriesb)")} TT <- length(seriesa) cofa <- cofb <- NULL for (i in k:(100-k)){ # The workhorse: lm0 <- summary(rq(seriesa~seriesb,tau=(i/100))) lm1 <- summary(rq(seriesb~seriesa,tau=(i/100))) cofa[i-k+1] <- lm0$coef[2,1] cofb[i-k+1] <- lm1$coef[2,1] } return(list(cofa=cofa,cofb=cofb)) } |
* The first sentence is a quote by Michael Lewis.









May I ask how to add color to the Corner_text function, Sir?
Thank you
cornertext <- function(corner = "bottomright", y.intersp = 5, textt, col = "add your color here") { graphics:::legend( corner, textt, lty = NA, lwd = 2, bty = "n", pch = NA, inset = 0, y.intersp = y.intersp, ... ) }