When you google “Kurtosis”, you encounter many formulas to help you calculate it, talk about how this measure is used to evaluate the “peakedness” of your data, maybe some other measures to help you do so, maybe all of a sudden a side step towards Skewness, and how both Skewness and Kurtosis are higher moments of the distribution. This is all very true, but maybe you just want to understand what does Kurtosis mean and how to interpret this measure. Similarly to the way you interpret standard deviation (the average distance from the average). Here I take a shot at giving a more intuitive interpretation.
It is true that Kurtosis is used to evaluate the “peakedness” of your data, but so what? what do you care Peaky or not Peaky? you are not picky. The answer is that you would like to know where does your variance come from. If your data is not peaky, the variance is distributed throughout, if your data is peaky, you have little variance close to the “center” and the origin of the variance is from the “sides” or what we call tails.
Calculating means and the variances provides you important information about the your data, namely:
- Where is it? (mean)
- How scattered is it? (variance)
You can get more, you can also get a clue about the cause for the variance. In what way is your data scattered? Might be that your data has high standard deviation, yet the distribution is relatively flat, with just a handful of observations in the tails. That is why you want to take a look at the Kurtosis measure.
The next figure presents three simulated known distributions, Uniform, Normal and Laplace.
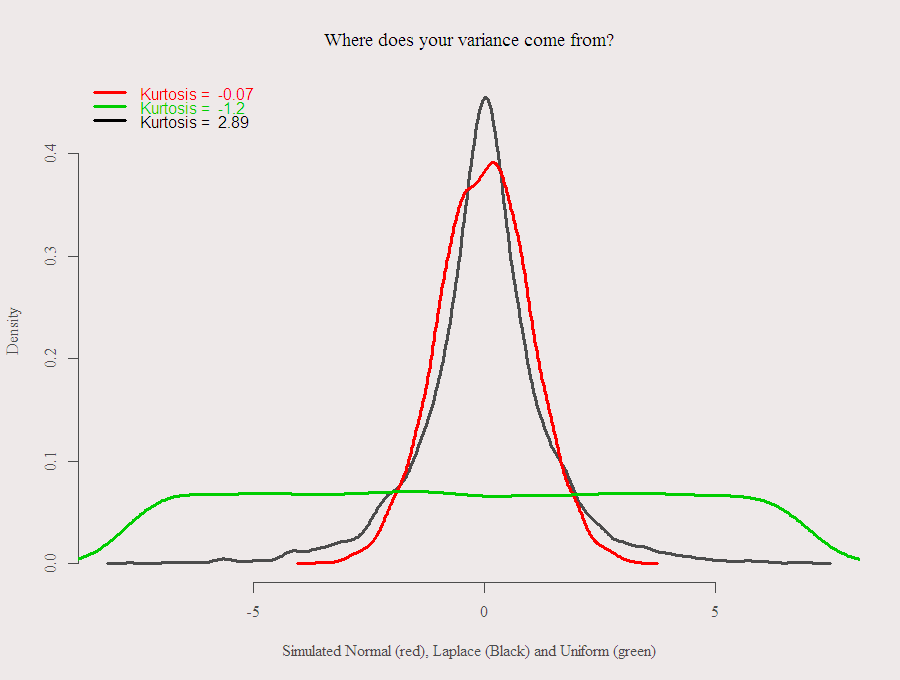The Uniform distribution has the highest Standard deviation (4.26 for this simulation), it is the most scattered one, but the lowest Kurtosis, (-1.2) since the variance is relatively “equally distributed”, the Laplace one has the highest Kurtosis, since the variance is most scattered, low portion of the variance comes from the center, that is the peakedness referred to earlier, and large portion of the variance comes from the tails. Code for the simulation and graph is below, thanks for reading.
Notes:
Kurtosis here is Excess Kurtosis, add 3 to get the actual Kurtosis.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
library(VGAM) # for the laplace lap = rlaplace(5000, location=0, scale=1) uni = runif(5000, min(lap),max(lap)) nor = rnorm(5000) denlap = density(lap);dennor = density(nor); denuni = density(uni ) lwd1 = 3 plot(denlap, lwd = lwd1, zer = F, main = "Where does your variance come from?", xlab = "Simulated Normal (red), Laplace (Black) and Uniform (green)") lines(dennor, col = 2, lwd = lwd1) lines(denuni, col = 3, lwd = lwd1) legend("topleft", c(paste("Kurtosis = ",round(kurtosis(nor),digits = 2)), paste("Kurtosis = ",round(kurtosis(uni),digits = 2)), paste("Kurtosis = ",round(kurtosis(lap), digits = 2))), col = c(2,3,1), lty = 1, lwd = lwd1, text.col = c(2,3,1), bty = "n") |
Related:
[asa onelinertpl]1441955240[/asa]
[asa onelinertpl]041587291X[/asa]
[asa onelinertpl]0321629302[/asa]
What follows is a clear explanation of why “peakedness” is simply wrong as a descriptor of kurtosis.
Suppose someone tells you that they have calculated negative excess kurtosis either from data or from a probability distribution function (pdf). According to the “peakedness” dogma (started unfortunately by Pearson in 1905), you are supposed to conclude that the distribution is “flat-topped” when graphed. But this is obviously false in general. For one example, the beta(.5,1) has an infinite peak and has negative excess kurtosis. For another example, the 0.5*N(0, 1) + 0.5*N(4,1) distribution is bimodal (wavy); not flat at all, and also has negative excess kurtosis. These are just two examples out of an infinite number of other non-flat-topped distributions having negative excess kurtosis.
Yes, the uniform (U(0,1)) distribution is flat-topped and has negative excess kurtosis. But obviously, a single example does not prove the general case. If that were so, we could say, based on the beta(.5,1) distribution, that negative excess kurtosis implies that the pdf is “infinitely pointy.” We could also say, based on the 0.5*N(0, 1) + 0.5*N(4,1) distribution, that negative excess kurtosis implies that the pdf is “wavy.” It’s like saying, “well, I know all bears are mammals, so it must be the case that all mammals are bears.”
Now suppose someone tells you that they have calculated positive excess kurtosis from either data or a pdf. According to the “peakedness” dogma (again, started by Pearson in 1905), you are supposed to conclude that the distribution is “peaked” or “pointy” when graphed. But this is also obviously false in general. For example, take a U(0,1) distribution and mix it with a N(0,1000000) distribution, with .00001 mixing probability on the normal. The resulting distribution, when graphed, appears perfectly flat at its peak, but has very high kurtosis.
You can play the same game with any distribution other than U(0,1). If you take a distribution with any shape peak whatsoever, then mix it with a much wider distribution like N(0,1000000), with small mixing probability, you will get a pdf with the same shape of peak (flat, bimodal, trimodal, sinusoidal, whatever) as the original, but with high kurtosis.
And yes, the Laplace distribution has positive excess kurtosis and is pointy. But you can have any shape of the peak whatsoever and have positive excess kurtosis. So the bear/mammal analogy applies again.
One thing that can be said about cases where the data exhibit high kurtosis is that when you draw the histogram, the peak will occupy a narrow vertical strip of the graph. The reason this happens is that there will be a very small proportion of outliers (call them “rare extreme observations” if you do not like the term “outliers”) that occupy most of the horizontal scale, leading to an appearance of the histogram that some have characterized as “peaked” or “concentrated toward the mean.”
But the outliers do not determine the shape of the peak. When you zoom in on the bulk of the data, which is, after all, what is most commonly observed, you can have any shape whatsoever – pointy, inverted U, flat, sinusoidal, bimodal, trimodal, etc.
So, given that someone tells you that there is high kurtosis, all you can legitimately infer, in the absence of any other information, is that there are rare, extreme data points (or potentially observable data points). Other than the rare, extreme data points, you have no idea whatsoever as to what is the shape of the peak without actually drawing the histogram (or pdf), and zooming in on the location of the majority of the (potential) data points.
And given that someone tells you that there is negative excess kurtosis, all you can legitimately infer, in the absence of any other information, is that the outlier characteristic of the data (or pdf) is less extreme than that of a normal distribution. But you will have no idea whatsoever as to what is the shape of the peak, without actually drawing the histogram (or pdf).
The logic for why the kurtosis statistic measures outliers (rare, extreme observations in the case of data; potential rare, extreme observations in the case of a pdf) rather than the peak is actually quite simple. Kurtosis is the average (or expected value in the case of the pdf) of the
Z-values, each taken to the 4th power. In the case where there are (potential) outliers, there will be some extremely large Z^4
values, giving a high kurtosis. If there are less outliers than, say, predicted by a normal pdf, then the most extreme Z^4 values will not be particularly large, giving smaller kurtosis.
What of the peak? Well, near the peak, the Z^4
values are extremely small and contribute very little to their overall average (which again, is the kurtosis). That is why kurtosis tells you virtually nothing about the shape of the peak. I give mathematical bounds on the contribution of the data near the peak to the kurtosis measure in the following article:
Kurtosis as Peakedness, 1905 – 2014. R.I.P. The American Statistician, 68, 191–195.
I hope this helps.
@Peter, Great comment. Thank You.