For those of you who are into machine learning, here you can find a cool collection of databases to play around with your favorite algorithm. I choose one out of the available 200 and fit a logistic regression model. The idea is to see what kind of properties are common for those who earn above 50K a year. Our data is such that the “y” variable is binary. A value of 1 is given if the individual earns above 50K and 0 if below. We know many things about the individual. Level of education in years, age, is she married, where from, which sector is she working in, how many working hours per week, race, and more. We can fit logistic regression, which is quite standard for a binary dependent variable, and see which variables are important.
Result:
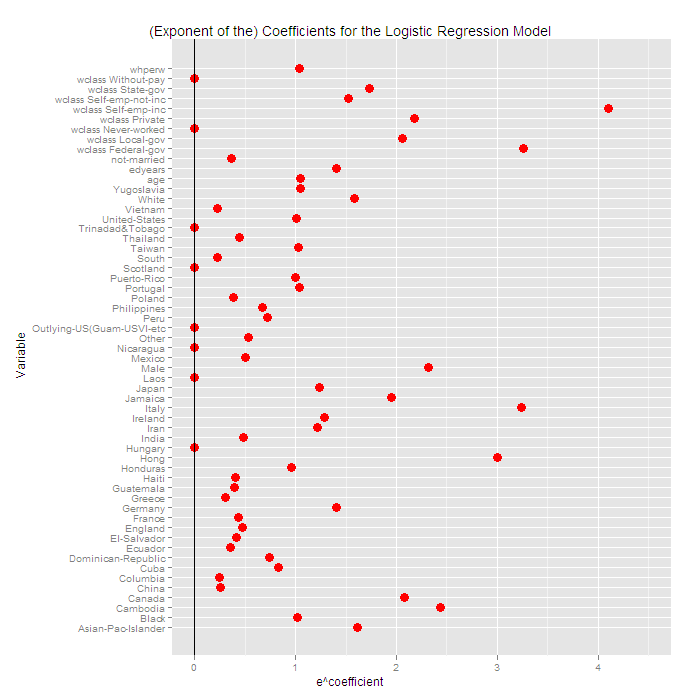A variable between 0 and 1 means that it has negative influence on the probability to earn above 50K. The higher the coefficient the more positive influence it has. However, most of the coefficients are insignificant:
| Estimate | Std. Error | z value | P.val | |
|---|---|---|---|---|
| (Intercept) | -8.9309 | 0.4451 | -20.06 | 0.0000 |
| age | 0.0428 | 0.0021 | 20.57 | 0.0000 |
| edyears | 0.3427 | 0.0115 | 29.85 | 0.0000 |
| whperw | 0.0321 | 0.0022 | 14.33 | 0.0000 |
| not-married | -1.0096 | 0.0550 | -18.37 | 0.0000 |
| Cambodia | 0.8904 | 0.8982 | 0.99 | 0.3216 |
| Canada | 0.7303 | 0.3816 | 1.91 | 0.0556 |
| China | -1.3751 | 0.6159 | -2.23 | 0.0256 |
| Columbia | -1.4248 | 0.9515 | -1.50 | 0.1343 |
| Cuba | -0.1931 | 0.5177 | -0.37 | 0.7091 |
| Dominican-Republic | -0.3022 | 0.8232 | -0.37 | 0.7136 |
| Ecuador | -1.0433 | 1.3723 | -0.76 | 0.4471 |
| El-Salvador | -0.8846 | 0.7955 | -1.11 | 0.2661 |
| England | -0.7531 | 0.4852 | -1.55 | 0.1207 |
| France | -0.8418 | 1.1822 | -0.71 | 0.4764 |
| Germany | 0.3424 | 0.3910 | 0.88 | 0.3812 |
| Greece | -1.1965 | 0.6605 | -1.81 | 0.0701 |
| Guatemala | -0.9350 | 1.1504 | -0.81 | 0.4164 |
| Haiti | -0.9143 | 1.1334 | -0.81 | 0.4199 |
| Honduras | -0.0409 | 1.3071 | -0.03 | 0.9750 |
| Hong Kong | 1.0995 | 1.2604 | 0.87 | 0.3830 |
| Hungary | -12.8463 | 882.7434 | -0.01 | 0.9884 |
| India | -0.7264 | 0.4826 | -1.51 | 0.1323 |
| Iran | 0.1945 | 0.5350 | 0.36 | 0.7161 |
| Ireland | 0.2540 | 0.7516 | 0.34 | 0.7353 |
| Italy | 1.1770 | 0.5147 | 2.29 | 0.0222 |
| Jamaica | 0.6685 | 0.5289 | 1.26 | 0.2063 |
| Japan | 0.2082 | 0.5782 | 0.36 | 0.7187 |
| Laos | -12.3934 | 432.8021 | -0.03 | 0.9772 |
| Mexico | -0.6878 | 0.3607 | -1.91 | 0.0566 |
| Nicaragua | -12.3164 | 244.3564 | -0.05 | 0.9598 |
| Guam-USVI-etc | -12.5394 | 421.4650 | -0.03 | 0.9763 |
| Peru | -0.3240 | 1.1425 | -0.28 | 0.7767 |
| Philippines | -0.4033 | 0.4323 | -0.93 | 0.3509 |
| Poland | -0.9650 | 0.6266 | -1.54 | 0.1236 |
| Portugal | 0.0386 | 0.8386 | 0.05 | 0.9632 |
| Puerto-Rico | -0.0004 | 0.5131 | -0.00 | 0.9994 |
| Scotland | -12.5727 | 447.6334 | -0.03 | 0.9776 |
| South | -1.4788 | 0.6520 | -2.27 | 0.0233 |
| Taiwan | 0.0304 | 0.5518 | 0.06 | 0.9560 |
| Thailand | -0.8068 | 0.9884 | -0.82 | 0.4143 |
| Trinadad& Tobago | -12.2504 | 307.6617 | -0.04 | 0.9682 |
| United-States | 0.0049 | 0.1879 | 0.03 | 0.9791 |
| Vietnam | -1.5021 | 0.8277 | -1.81 | 0.0696 |
| Yugoslavia | 0.0495 | 1.3221 | 0.04 | 0.9702 |
| Federal-gov | 1.1812 | 0.1939 | 6.09 | 0.0000 |
| Local-gov | 0.7243 | 0.1714 | 4.23 | 0.0000 |
| Never-worked | -9.7524 | 618.4062 | -0.02 | 0.9874 |
| Private | 0.7785 | 0.1491 | 5.22 | 0.0000 |
| Self-emp-inc | 1.4118 | 0.1863 | 7.58 | 0.0000 |
| Self-emp-not-inc | 0.4238 | 0.1678 | 2.53 | 0.0115 |
| State-gov | 0.5512 | 0.1887 | 2.92 | 0.0035 |
| Without-pay | -10.6696 | 622.2566 | -0.02 | 0.9863 |
| Asian-Pac-Islander | 0.4790 | 0.3931 | 1.22 | 0.2230 |
| Black | 0.0179 | 0.3375 | 0.05 | 0.9576 |
| race – Other | -0.6295 | 0.5792 | -1.09 | 0.2771 |
| White | 0.4567 | 0.3230 | 1.41 | 0.1573 |
| Male | 0.8382 | 0.0643 | 13.05 | 0.0000 |
So… what is important?
- We can see that males has better chance to earn more.
- Nice to see that race is not important, e.g. being black has no significant effect.
- Government is a good thing.
- Being self employed is a good thing.
- Being from Italy is good thing.. 😮
- working hard is a good thing, “whperw” is working hours per week. However, the value of the coefficient is not high, so don’t work too hard.
- Older is better, again, the coefficient, despite its importance, is not high.
- Being educated is important. “edyears” is of years of schooling.
- Being married is important. :-D, if you are not married there is a significant negative impact on the chance to earn more than 50K per year.
Notes:
We have a serious endogeneity problem here, in more than one place. For example, you probably wait until you have some money saved in order to get marry to begin with. As another example, you probably open your own company only after you earn enough so that you pay less taxes as a company inc.
So, we can interpret these results more as common features shared by the rich group, and less for causality. It can be used for example to slice the market into potential buyers (people with money), according to their characteristics without the need to go into their bank account statement. Thanks for reading, code and references below.
Related:
[asa onelinertpl]0521848059[/asa]
[asa onelinertpl]0691120358[/asa]
[asa onelinertpl]0324581629[/asa]
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
t2 = read.table("/incomedat.txt", sep = ",", header = F) ## Some bookkeeping, drop what we don't use, rename what we do. head(t2, 4) ; dim(t2) ; names(t2) ; class(t2) t2 = t2[-NROW(t2),-c(3,4,8,11,12)] summary(t2) names(t2)<-c("age","wclass","edyears","mstatus","occ","race","gender","whperw","region","y") mstatus = NULL mstatus[as.numeric(t2$mstatus)==c(3,4)]<-"married" mstatus[as.numeric(t2$mstatus)!=c(3,4)]<-"not-married" head(mstatus) t2$mstatus <-as.factor(mstatus) levels(t2$mstatus) y = as.factor(as.numeric(t2$y) - 2) t2$y = y ; levels(t2$y) train = t2[1:round(NROW(t2)*(2/3)),] test = t2[(round(NROW(t2)*(2/3))+1):NROW(t2),] # We might want to forecast later dim(train) ; dim(test) names(train) ; class(train) lm2 = glm(train$y ~ train$age+ train$edyears+train$whperw+as.factor(train$mstatus)+ as.factor(train$region)+ (train$wclass)+ as.factor(train$race)+as.factor(train$gender), family = binomial(link = "logit"),na.action = na.pass) summary(lm2) |
Consider plotting the coefficients from greatest to least effect. In ggplot2 you can do this by reordering the levels of the names of your coefficients. See ?reorder.
Hit Post too soon.
Also, you can show that most variables are insignificant by plotting error bars using geom_errorbar(), geom_segment(), etc. I recommend posting your plotting code as well.
Hi Erik,
Thanks, those are good comments.
The code for the plot is messy as I chopped out code from here:
http://diffuseprior.wordpress.com/2012/04/23/probitlogit-marginal-effects-in-r-2/
which refers to another code from here:
http://ideas.repec.org/p/ucn/wpaper/201122.html
But I will use your suggestions next time.
Cool, an interesting analysis. To follow-up on eshilts’s comment on error bars, this kind of study might be subject to the Texas-Sharpshooter’s fallacy, and there may need to be a multiple comparisons correction for the confidence intervals.
Cheers,
Fred