Tag: risk

Beta in the tails

Blog, Finance and Trading, Risk, Statistics and EconometricsPosted on

Every form of strength is also a form of weakness*. I love statistics, but I focus to much on methodology, which is not for everyone. Some people (right or wrong) question: “wonderful sir, but what can I do with it?”.

A new paper titled “Beta in the tails” is a showcase application for why we should focus on correlation structure rather than on average correlation. They discuss the question: Do hedge funds hedge? The reply: No, they don’t!

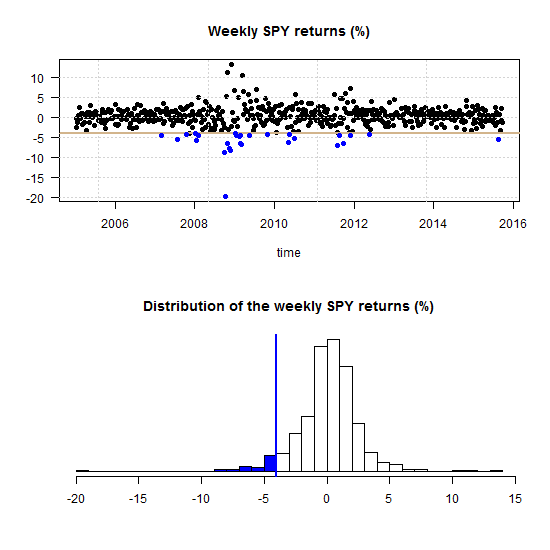
The paper “Beta in the tails” was published in the Journal of Econometrics but you can find a link to a working paper version below. We start with a figure replicated from the paper, go through the meaning and interpretation of it, and explain the methods used thereafter.

Continue reading

Adaptive Huber Regression

Blog, Finance and Trading, Risk, Statistics and EconometricsPosted on

Many years ago, when I was still trying to beat the market, I used to pair-trade. In principle it is quite straightforward to estimate the correlation between two stocks. The estimator for beta is very important since it determines how much you should long the one and how much you should short the other, in order to remain market-neutral. In practice it is indeed very easy to estimate, but I remember I never felt genuinely comfortable with the results. Not only because of instability over time, but also because the Ordinary Least Squares (OLS from here on) estimator is theoretically justified based on few text-book assumptions, most of which are improper in practice. In addition, the OLS estimator it is very sensitive to outliers. There are other good alternatives. I have described couple of alternatives here and here. Here below is another alternative, provoked by a recent paper titled Adaptive Huber Regression.

Continue reading

Create own Recession Indicator using Mixture Models

Blog, Finance and Trading, Statistics and EconometricsPosted on

Context

Broadly speaking, we can classify financial markets conditions into two categories: Bull and Bear. The first is a “todo bien” market, tranquil and generally upward sloping. The second describes a market with a downturn trend, usually more volatile. It is thought that those bull\bear terms originate from the way those animals supposedly attack. Bull thrusts its horns up while a bear swipe its paws down. At any given moment, we can only guess the state in which we are in, there is no way of telling really; simply because those two states don’t have a uniformly exact definitions. So basically we never actually observe a membership of an observation. In this post we are going to use (finite) mixture models to try and assign daily equity returns to their bull\bear subgroups. It is essentially an unsupervised clustering exercise. We will create our own recession indicator to help us quantify if the equity market is contracting or not. We use minimal inputs, nothing but equity return data. Starting with a short description of Finite Mixture Models and moving on to give a hands-on practical example.

Continue reading

Curse of dimensionality part 3: Higher-Order Comoments

Blog, Finance and Trading, Statistics and EconometricsPosted on

Higher moments such as Skewness and Kurtosis are not as explored as they should be.

These moments are crucial for managing portfolio risk. At least as important as volatility, if not more. Skewness relates to asymmetry risk and Kurtosis relates to tail risk.

Despite their great importance, those higher moments enjoy only a small portion of attention compared with their lower more friendly moments: the mean and the variance. In my opinion, one reason for this may be the impossibility of estimating those moments, estimating them accurately that is.

It is yet another situation where Curse of Dimensonality rears its enchanting head (and an idea for a post is born..).

Continue reading

Visualizing Tail Risk

Blog, Finance and Trading, RiskPosted on

Tail risk conventionally refers to the risk of a large and sharp draw down of the portfolio. How large is subjective and depends on how you define what is a tail.

A lot of research is directed towards having a good estimate of the tail risk. Some fairly new research also now indicates that investors perceive tail risk to be a stand-alone risk to be compensated for, rather than bundled together with the usual variability of the portfolio. So this risk now gets even more attention.

Continue reading

Outliers and Loss Functions

Blog, Risk, Statistics and EconometricsPosted on

A few words about outliers

In statistics, outliers are as thorny topic as it gets. Is it legitimate to treat the observations seen during global financial crisis as outliers? or are those simply a feature of the system, and as such are integral part of a very fat tail distribution?

Continue reading

Density Confidence Interval

Blog, Finance and Trading, Risk, Statistics and EconometricsPosted on

Density estimation belongs with the literature of non-parametric statistics. Using simple bootstrapping techniques we can obtain confidence intervals (CI) for the whole density curve. Here is a quick and easy way to obtain CI’s for different risk measures (VaR, expected shortfall) and using what follows, you can answer all kind of relevant questions.

Continue reading

Modeling Tail Behavior with EVT

Blog, Risk, Statistics and EconometricsPosted on

Extreme Value Theory (EVT) and Heavy tails

Extreme Value Theory (EVT) is busy with understanding the behavior of the distribution, in the extremes. The extreme determine the average, not the reverse. If you understand the extreme, the average follows. But, getting the extreme right is extremely difficult. By construction, you have very few data points. By way of contradiction, if you have many data points then it is not the extreme you are dealing with.

Continue reading

Multivariate Volatility Forecast Evaluation

Blog, Finance and Trading, Risk, Statistics and EconometricsPosted on

The evaluation of volatility models is gracefully complicated by the fact that, unlike other time series, even the realization is not observable. Two researchers would never disagree about what was yesterday’s stock price, but they can easily disagree about what was yesterday’s stock volatility. Because we don’t observe volatility directly, each of us uses own proxy of choice. There are many ways to skin this cat (more on volatility proxy here).

In a previous post Univariate volatility forecast evaluation we considered common ways in which we can evaluate how good is our volatility model, dealing with one time-series at a time. But how do we evaluate, or compare two models in a multivariate settings, with two covariance matrices?

Continue reading

Why bad trading strategies may perform well? Mathematical explanation

Blog, Finance and Trading, Risk, Statistics and EconometricsPosted on

You probably know that even a trading strategy which is actually no different from a random walk (RW henceforth) can perform very well. Perhaps you chalk it up to short-run volatility. But in fact there is a deeper reason for this to happen, in force. If you insist on using and continuously testing a RW strategy, you will find, at some point with certainty, that it has significant outperformance.

This post explains why is that.

Continue reading

Correlation and correlation structure (3), estimate tail dependence using regression

Blog, Finance and Trading, Risk, Statistics and EconometricsPosted on

What is tail dependence really? Say the market had a red day and saw a drawdown which belongs with the 5% worst days (from now on simply call it a drawdown):
weekly SPY returns
One can ask what is now, given that the market is in the blue region, the probability of a a drawdown in a specific stock?

Continue reading