Volatility is unobserved. Hence we need to use observed quantity as a proxy. Every once in a while I still see people using squared daily return as a proxy. However, there is ample evidence that it is a bad one. Bad in a sense that it is noisy, which means that although on average it is a good estimate, on any individual day the estimate can be very far from the actual unobserved volatility. Here is a figure of the alleged standard deviation in the form of (square root of the) squared daily return for the recent year:
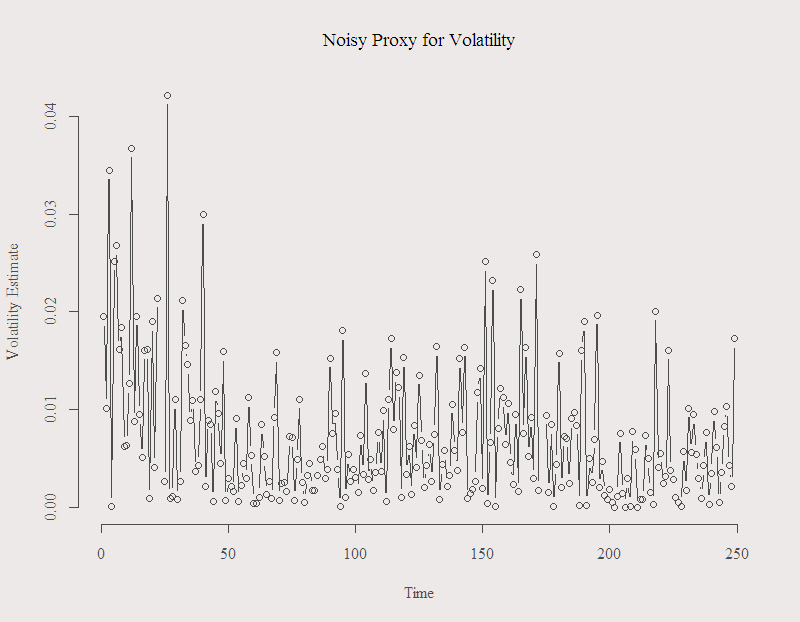You can see that in many days, this noisy estimate suggests that the volatility was around 2% and more. To me, it does not make too much sense. The series is the S&P 500, so a move of 3% is a BIG one. You can also see how “jumpy” the series is. The figure illustrates why we should avoid using this estimate.
Forecasting the Misery Index, follow-up
Five months ago I generated forecasts for the Eurozone Misery index. I used the built-in “FitAR” package in R. Using different models differing in their memory length (how many lags were considered for each model) 24 months ahead forecasts were generated. Might be interesting to see how accurate are the forecasts. The previous post is updated and few bugs corrected in the code. The updated data is public and can be found here. It is the sum of inflation rate and unemployment rate in the Euro-zone area.
Volatility forecast evaluation in R
In portfolio management, risk management and derivative pricing, volatility plays an important role. So important in fact that you can find more volatility models than you can handle (Wikipedia link). What follows is to check how well each model performs, in and out of sample. Here are three simple things you can do:
Intraday volatility measures
In the last few decades there has been tremendous progress in the realm of volatility estimation. A major step is the additional use of intraday price path. It has been shown that estimates which consider intraday information are more accurate. Which is to say they converge faster to the real unobserved value of the true volatility.
Behavioral Economics in Action
Do doctors unnecessarily prolong Colonoscopy? the answer is: they surely might.
A shrinkage estimator for beta
In the post pairs trading issues one of the problems raised was the unstable estimates of the stock’s beta with respect to the market. Here is a suggestion for a possible solution, which is not really a solution but more stuff to do to make you feel less stupid when trading based on your fragile estimates.
Information Criteria for Autoregression
Some knowledge about the bootstrapping procedure is assumed.
In time series analysis, Information Criteria can be found under every green tree. These are function to help you determine when to stop adding explanatory variables to your model.
Bootstrapping time series – R code
Bootstrapping in its general form (“ordinary” bootstrap) relies on IID observations which staples the theory backing it. However, time series are a different animal and bootstrapping time series requires somewhat different procedure to preserve dependency structure.
Better summary function in R
The summary function in R returns:
|
1 2 3 4 5 |
summary(x) Min. 1st Qu. Median Mean 3rd Qu. Max. 9.14 10.70 11.10 11.30 12.10 13.60 |
For the univariate case I wrote what I consider to be a better summary function which returns:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
usum(x) # For univariate Summary Summary Statistics: min med mean max sd skew kurt 1 9.14 11.13 11.35 13.65 1.057 0.3028 -0.6389 ------ NA's?: No NA's in the series ------ Head Tail 13.65 13.55 13.08 13.13 ------ Length Class 207 numeric |
Random books
It seems like a very long while since my bachelor. Checking my bookshelf the other day I was thinking to flag some of those books which helped or inspired me along the way. Here they are in no particular order.
Forecasting the Eurozone Misery index
Is Miss Stagflation coming to visit?
The Misery index is the sum of inflation and unemployment rate. We would like them both to stay naturally low, and we are miserable when they are not. The index is currently floating in it’s record scratching levels. In this post I demonstrate the use of the nice FitAR package in R to fit an AR model and see what we can expect accordingly. Inflation and unemployment numbers concerning the Eurozone (17 countries) can be found here.
Have a look at the index over time:
Stock market Kurtosis over time
In the last decade we have observed an increase in computational power, information availability, speed of execution and stock market competition in general. One might think that, as a result, we are prone to larger shocks that occur faster than what was common in the past. I crunched some numbers and was surprised to see that this is not the case.
Kurtosis Interpretation
When you google “Kurtosis”, you encounter many formulas to help you calculate it, talk about how this measure is used to evaluate the “peakedness” of your data, maybe some other measures to help you do so, maybe all of a sudden a side step towards Skewness, and how both Skewness and Kurtosis are higher moments of the distribution. This is all very true, but maybe you just want to understand what does Kurtosis mean and how to interpret this measure. Similarly to the way you interpret standard deviation (the average distance from the average). Here I take a shot at giving a more intuitive interpretation.
Marriage is good for your income
For those of you who are into machine learning, here you can find a cool collection of databases to play around with your favorite algorithm. I choose one out of the available 200 and fit a logistic regression model. The idea is to see what kind of properties are common for those who earn above 50K a year. Our data is such that the “y” variable is binary. A value of 1 is given if the individual earns above 50K and 0 if below. We know many things about the individual. Level of education in years, age, is she married, where from, which sector is she working in, how many working hours per week, race, and more. We can fit logistic regression, which is quite standard for a binary dependent variable, and see which variables are important.
Backtesting trading strategies with R
Few weeks back I gave a talk about Backtesting trading strategies with R, got a few requests for the slides so here they are: