Multivariate volatility forecasting

Introduction

When hopping from univariate volatility forecasts to multivariate volatility forecast, we need to understand that now we have to forecast not only the univariate volatility element, which we already know how to do, but also the covariance elements, which we do not know how to do, yet. Say you have two series, then this covariance element is the off-diagonal of the 2 by 2 variance-covariance matrix. The precise term we should use is “variance-covariance matrix”, since the matrix consists of the variance elements on the diagonal and the covariance elements on the off-diagonal. But since it is very tiring to read\write “variance-covariance matrix”, it is commonly referred to as the covariance matrix, or sometimes less formally as var-covar matrix.

If you are still reading this, I can imagine you have some experience in modelling correlation. The link between correlation and covariance is direct, given that you know the variance $\sigma^2$ of the individual series:

$cor(x1,x2) = \frac{cov(x1,x2)}{\sigma_{x1} \sigma_{x2} }.$

So when I first looked at this subject I did not understand why do we need the colossal literature describing all kinds of multivariate models. Why not model all the off-diagonal individually, using for example a rolling window of the sample pairwise correlation? quickly replied, you want to have a valid correlation matrix, which means symmetric (easy enough to impose) and positive-semidefinite, also known as nonnegative-definite (not easy to impose).

First, why the nonnegative-definite property is important, and second, why it is not easy to impose. Think about nonnegative-definite imposition as the multivariate equivalent to the positivity imposition on volatility in the univariate case. You don’t want to have your machine spit out negative volatility do you? In the univariate case multiplying $\sigma$ by any squared number, we trivially remain in positive territory. In a higher dimension, ensuring “positivity” of the covariance involves multiplying, not by a squared scalar, but by a “squared” vector.

Denote XC as the centered random variable X, so $XC=x-\mu_x$ . Now by definition $COV.MAT=E[(XC)(XC^t)]$ is a covariance matrix, clearly nonnegative-definite. Now if we multiply the matrix by a “squared” vector, $v^t E[(XC)(XC^t)] v$ we can “insert” the vector into the expectation (because (1) the vector is not a random variable, and (2) linearity of the expectation operator). We (should) still get nonnegative-definite matrix: $E[(v^tXC)((v^tXC)^t)].$ It does not matter which vector $v$ you use, since it is “squared”. This is the origin to the algebraic reverse: A symmetric matrix $\Sigma$ of size $N$ is positive semi-definite if and only if $v^t \Sigma v \geq 0$ for all possible vectors $v$ (of size $N$ of course).

If we model the covariance entries individually, pairwisely, and “patch” them together into a matrix, placing each pairwise covariance in the right place (for example the covariance between variable 1 and variable 3 in entries $\{1,3\}$ and $\{3,1\}$ , there is no guarantee that we eventually end up with a nonnegative-definite matrix. Since there is no covariance matrix which is nonnegative-definite, then what we can potentially get an invalid covariance matrix. Practitioners, free from a tedious academic refereeing process, may get away with this theoretical blunder. However, in addition there are other problems, computational in nature. A nonnegative-definite matrix can have zero or negative determinant. In many Bayesian application we would like to use precision matrix instead of the covariance matrix. To compute precision matrix, we simply invert the covariance matrix, but this means that we divide by the determinant, so a determinant which is zero creates a problem if you are not Chuck Norris, who can supposedly divide by zero as the rumor goes.

The main building block in the literature is the GARCH process. Say we have a random variable $X1$ , we can model its volatility using:

(1) $\begin{equation*} \sigma^2_t = \omega + \alpha \varepsilon^2_{t-1} + \beta \sigma^2_{t-1}. \end{equation*}$

Easy enough to understand. What is important for the volatility today is the volatility yesterday $\sigma^2_{t-1}$ , with specific emphasis on the shock yesterday, $\varepsilon^2_{t-1}$ . Remember that if $E[\varepsilon_{t-1}] = 0,$ then $\varepsilon^2_{t-1}$ is simply an estimate of the variance of $\varepsilon_{t-1}$ only, without accounting for anything dating back past t-1.

Up the dimension

Now, add another random variable $X2$ . You now have 2 volatilities and a covariance term. But why not extend this process in the same way Vector Auto Regression (VAR) extends Auto regression? Enter VEC model:

(2) $\begin{equation*} vec(\Sigma_t) = vec(\Omega) + A vec(\varepsilon_{t-1} \varepsilon^ \prime_{t-1}) + B vec(\Sigma _{t-1}), \end{equation*}$

where $vec$ is a vectorize operator, taking a matrix and stacking it as a vector. Naturally, because of the symmetry of the matrix, we don’t need all the coefficients, so for clarity here is a better representation:

(3) $\begin{equation*} \sigma_{t} = \begin{pmatrix} \sigma_{11,t} \\ \sigma_{21,t}\\ \sigma_{22,t} \end{pmatrix} = \begin{pmatrix} \alpha_{11} & \alpha_{12} & \alpha_{13} \\ \alpha_{21} & \alpha_{22} & \alpha_{23} \\ \alpha_{31} & \alpha_{31} & \alpha_{33} \end{pmatrix} \begin{pmatrix} \varepsilon^2_{1,t-1} \\ \varepsilon_{1,t-1} \varepsilon_{2,t-1} \\ \varepsilon^2_{2,t-1} \end{pmatrix} + \begin{pmatrix} \beta_{11} & \beta_{12} & \beta_{13} \\ \beta_{21} & \beta_{22} & \beta_{23} \\ \beta_{31} & \beta_{31} & \beta_{33} \end{pmatrix} \begin{pmatrix} \sigma_{11,t-1} \\ \sigma_{21,t-1}\\ \sigma_{22,t-1} \end{pmatrix}. \end{equation*}$

The intuition behind this model is the same as that underlying the VAR. Maybe when volatility of equities is high, volatility in bonds is lower, maybe when volatility in bonds is high, covariance with equities is high, etc.

A potential problem with this model, also analogues to the VAR, is that maybe volatilities are independent processes, meaning that only the diagonal of A and B matters, in which case we simply trouble the model with unnecessary estimation noise. Another computational issue mentioned before, is that since we do not model the matrix-process per se, but the three terms one by one, we don’t ensure the result is a valid covariance matrix, in particular no nonnegative-definite constraint is imposed. The BEKK model (Baba, Engle, Kraft and Kroner, 1990) makes this advancement, the curious reader is referred to the original paper. There is a good reason not to discuss those “first-generation” models in length. They are very difficult to estimate for more than a handful of variables. I have not tried those personally, it is a hearsay from those unfortunate souls who did. For those models, even if one is successful in estimation, the complications in estimation casts a heavy shadow on the results as far as practitioners are concerned.

CCC and DCC

A surge in the literature followed the next sizable step delivered by Engle (2002) in his seminal paper: “Dynamic Conditional Correlation: A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models”. From the abstract: “These (models) have the flexibility of univariate GARCH models coupled with parsimonious parametric models for the correlations.” Key entry point to this class of conditional correlation models is to realize that

(4) $\begin{equation*} \Sigma_t = D_t R_t D_t, \end{equation*}$

with $D_t$ being a matrix with the volatility of the individual series (now estimated individually) on the diagonal and zeros off-diagonal. This is just a manipulation in matrix form of the usual equation we started with: $\mathrm{corr}(X,Y)={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y}$ , since $R_t=D^{-1}_t \Sigma_t D^{-1}_t$ . Now few things are in place:

You separate the diagonal from the off-diagonal in $\Sigma$ . You can “fill-in” the diagonal using the usual univariate GARCH estimates. The off diagonal is given by the correlation matrix, on which we can now decide. When we assume a constant correlation matrix (CCC), meaning $R_t = R$ , we can naturally use the sample correlation matrix. We can assume the $R$ matrix is time-varying and estimate it using rolling window or exponentially decaying weights or in another way.

Because of the quadratic form $\Sigma_t = D_t R_t D_t$ and because $R$ is a correlation matrix, we are certain to get a valid covariance matrix, which is time varying even when we use constant correlation matrix.

Because of this separation, diagonal from off-diagonal, we can actually handle many variables, very much unlike the “first-generation” class of models. This, I think, is the main reason for the acceptance and popularity of the model.

Now we estimate.

Estimation using R

Let’s get some data. We pull the last few years of three ETF’s. The SPY (tracking the S&P 500), TLT and IEF (tracking long and medium term US bonds respectively).


library(quantmod)
k <- 3 # how many years back?
end<- format(Sys.Date(),"%Y-%m-%d") 
end_training <- "2015-01-01"
start<-format(Sys.Date() - (k*365),"%Y-%m-%d")
sym = c('SPY', 'TLT', "IEF") # S&P 500, long and medium term bonds, all ETFs
l <- length(sym)
dat0 = getSymbols(sym[1], src="yahoo", from=start, to=end, auto.assign = F, warnings = FALSE,symbol.lookup = F)
n = NROW(dat0)  
dat = array(dim = c(n,NCOL(dat0),l)) ; ret = matrix(nrow = n, ncol = l) 
for (i in 1:l){
  dat0 = getSymbols(sym[i], src="yahoo", from=start, to=end, auto.assign = F,warnings = FALSE,symbol.lookup = F)
  dat[1:n,,i] = dat0 
  ret[2:n,i] = (dat[2:n,4,i]/dat[1:(n-1),4,i] - 1) # returns, close to close, percent
}
ret <- na.omit(ret)# Remove the first observation
time <- index(dat0)[-1]
TT <- NROW(ret)
colnames(ret) <- sym

library(quantmod)

k <- 3 # how many years back?

end<- format(Sys.Date(),"%Y-%m-%d")

end_training <- "2015-01-01"

start<-format(Sys.Date() - (k*365),"%Y-%m-%d")

sym = c('SPY', 'TLT', "IEF") # S&P 500, long and medium term bonds, all ETFs

l <- length(sym)

dat0 = getSymbols(sym[1], src="yahoo", from=start, to=end, auto.assign = F, warnings = FALSE,symbol.lookup = F)

n = NROW(dat0)

dat = array(dim = c(n,NCOL(dat0),l)) ; ret = matrix(nrow = n, ncol = l)

for (i in 1:l){

dat0 = getSymbols(sym[i], src="yahoo", from=start, to=end, auto.assign = F,warnings = FALSE,symbol.lookup = F)

dat[1:n,,i] = dat0

ret[2:n,i] = (dat[2:n,4,i]/dat[1:(n-1),4,i] - 1) # returns, close to close, percent

}

ret <- na.omit(ret)# Remove the first observation

time <- index(dat0)[-1]

TT <- NROW(ret)

colnames(ret) <- sym

Now to demonstrate how to construct covariance matrix using the CCC and DCC models. We first get the univariate volatilities. We need them, they sit on the diagonal of the diagonal matrix $D_t$ . We estimate them using asymmetric GARCH with heavy tails.


library(rugarch) # Alexios Ghalanos (2014). rugarch: Univariate GARCH models. R package version 1.3-4.
gjrtspec <- ugarchspec(mean.model=list(armaOrder=c(1,0)),variance.model =list(model = "gjrGARCH"),distribution="std") # std is student t distribution
Uvolatility_fit <- matrix(nrow=(TT),ncol=l) # container of a matrix to hold the volatilities of the three assets
for (i in 1:l){
  Tgjrmodel = ugarchfit(gjrtspec,ret[,i])
  Uvolatility_fit[,i] = as.numeric(sigma(Tgjrmodel))
}

library(rugarch) # Alexios Ghalanos (2014). rugarch: Univariate GARCH models. R package version 1.3-4.

gjrtspec <- ugarchspec(mean.model=list(armaOrder=c(1,0)),variance.model =list(model = "gjrGARCH"),distribution="std") # std is student t distribution

Uvolatility_fit <- matrix(nrow=(TT),ncol=l) # container of a matrix to hold the volatilities of the three assets

for (i in 1:l){

Tgjrmodel = ugarchfit(gjrtspec,ret[,i])

Uvolatility_fit[,i] = as.numeric(sigma(Tgjrmodel))

}

Now, once we have the meat in the sandwich $\Sigma_t = D_t R_t D_t$ , we are able to create the CCC and DCC-based covariance matrices. For the CCC (constant conditional correlation), we use the sample correlation matrix, and for the DCC (dynamic..), we use correlation matrix which is estimated based on a moving window of say 3 months.


# create a the covariance of the CCC model
nassets <- l # for better readability, the l looks too much like 1.
# make containers for the matrices over time:
samp_cor_tv <- cov_dcc <- cov_ccc <- array(dim=c(nassets, nassets, TT)) 
# Compute the sample unconditional correlation matrix:
samp_cor <- cor(ret) # will remain constant throughout the loop
wind <- 60 # roughly three months
for (i in (wind+1):TT){
dt <- (Uvolatility_fit[i,])*diag(nassets)
cov_ccc[,,i] <- dt %*% samp_cor %*% dt
samp_cor_tv[,,i] <- cor(ret[(i-wind):i,])
cov_dcc[,,i] <- dt %*% samp_cor_tv[,,i] %*% dt
}

# create a the covariance of the CCC model

nassets <- l # for better readability, the l looks too much like 1.

# make containers for the matrices over time:

samp_cor_tv <- cov_dcc <- cov_ccc <- array(dim=c(nassets, nassets, TT))

# Compute the sample unconditional correlation matrix:

samp_cor <- cor(ret) # will remain constant throughout the loop

wind <- 60 # roughly three months

for (i in (wind+1):TT){

dt <- (Uvolatility_fit[i,])*diag(nassets)

cov_ccc[,,i] <- dt %*% samp_cor %*% dt

samp_cor_tv[,,i] <- cor(ret[(i-wind):i,])

cov_dcc[,,i] <- dt %*% samp_cor_tv[,,i] %*% dt

}

Results

results are annualized and multiplied by 100 to move to percentage points for better readability. Plot it:


lwd1 <- 2
ann_percent <- 252*100
par()$mar # Margins are too wide for my taste
par(mfrow = c(2,1),mar=c(3.8,4.4,2.4,2.4))
plot(ann_percent*cov_ccc[1,1,]~time,ty="l",main="Annulaized variance, %",ylab="",lwd=lwd1,bty="o",
     cex.main=1.5,xlab="")
lines(ann_percent*cov_ccc[2,2,]~time, lwd=lwd1, col=2)
lines(ann_percent*cov_ccc[3,3,]~time, lwd=lwd1, col=3)
grid(col="blue")
legend("topleft", sym,col=1:3,lwd=lwd1,cex=1.1,bty="n",text.col=1:3)

plot(ann_percent*cov_ccc[1,2,]~time,ty="l",main="Annulaized covariance, %",ylab="",lwd=lwd1,bty="o",
     cex.main=1.5,xlab="",ylim=c(-2.5,1))
lines(ann_percent*cov_ccc[1,3,]~time, lwd=lwd1,col=2)
lines(ann_percent*cov_dcc[1,2,]~time, lwd=lwd1, col=1,lty=4)
lines(ann_percent*cov_dcc[1,3,]~time, lwd=lwd1, col=2,lty=4)
leg <-  c(paste("CCC-based covariance", sym[1], "with", sym[2]) , paste("CCC-based covariance", sym[1], "with", sym[3]))
legend("topleft",leg,col=1:2,lwd=lwd1,cex=1,bty="n",text.col=1:2)
leg <-  c(paste("DCC-based covariance", sym[1], "with", sym[2]) , paste("DCC-based covariance", sym[1], "with", sym[3]))
legend("topright",leg,col=1:2,lwd=lwd1,cex=1,bty="n",text.col=1:2,lty=4)
grid(col="blue")

lwd1 <- 2

ann_percent <- 252*100

par()$mar # Margins are too wide for my taste

par(mfrow = c(2,1),mar=c(3.8,4.4,2.4,2.4))

plot(ann_percent*cov_ccc[1,1,]~time,ty="l",main="Annulaized variance, %",ylab="",lwd=lwd1,bty="o",

cex.main=1.5,xlab="")

lines(ann_percent*cov_ccc[2,2,]~time, lwd=lwd1, col=2)

lines(ann_percent*cov_ccc[3,3,]~time, lwd=lwd1, col=3)

grid(col="blue")

legend("topleft", sym,col=1:3,lwd=lwd1,cex=1.1,bty="n",text.col=1:3)

plot(ann_percent*cov_ccc[1,2,]~time,ty="l",main="Annulaized covariance, %",ylab="",lwd=lwd1,bty="o",

cex.main=1.5,xlab="",ylim=c(-2.5,1))

lines(ann_percent*cov_ccc[1,3,]~time, lwd=lwd1,col=2)

lines(ann_percent*cov_dcc[1,2,]~time, lwd=lwd1, col=1,lty=4)

lines(ann_percent*cov_dcc[1,3,]~time, lwd=lwd1, col=2,lty=4)

leg <- c(paste("CCC-based covariance", sym[1], "with", sym[2]) , paste("CCC-based covariance", sym[1], "with", sym[3]))

legend("topleft",leg,col=1:2,lwd=lwd1,cex=1,bty="n",text.col=1:2)

leg <- c(paste("DCC-based covariance", sym[1], "with", sym[2]) , paste("DCC-based covariance", sym[1], "with", sym[3]))

legend("topright",leg,col=1:2,lwd=lwd1,cex=1,bty="n",text.col=1:2,lty=4)

grid(col="blue")

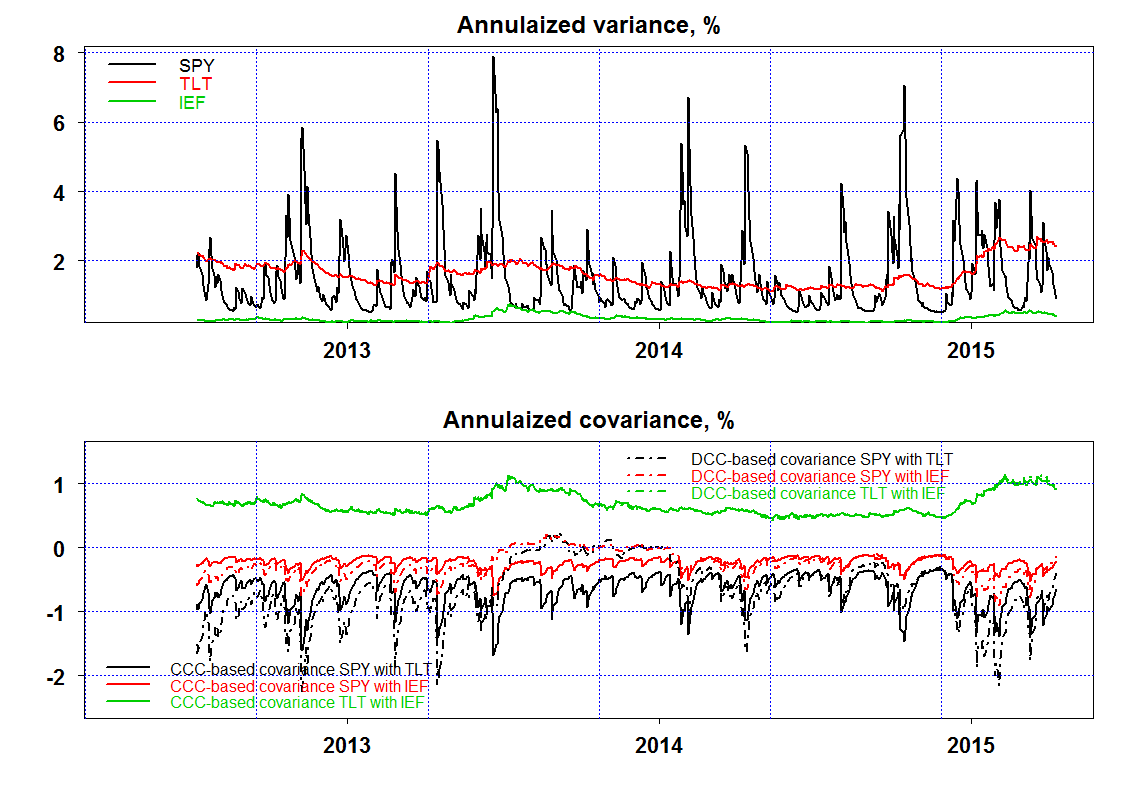
In the upper panel we have the diagonal of the covariance matrix. We see (1) the medium term bonds have the lowest volatility as expected, (2) SPY is volatile, and the variance of variance is also high (spiky-looking variance series). (3) the variance of the long end of the curve is higher than the variance of the medium term, which is a stylized fact in the yield curve literature. (4) Interestingly, the volatility of the long term bonds in US has been on the rise, probably a heightened sense of alert towards an impending(?) Fed hike in policy rates.

In the lower panel we have the covariance terms, all three of them, once estimated assuming CCC (solid) and once estimate assuming DCC (broken). For the covariance between the medium and long term bonds it does not matter much if you assume constant or dynamic correlation matrix. It does matter for the covariance terms of the SPY with the bonds however. For example, a DCC-based covariance matrix argue for almost zero covariance between stocks and bonds during mid 2013, while CCC-based suggest a more negative covariance during that period. Which is it, constant or dynamic, potentially matters a great deal for cross asset portfolio construction.

Side notes

We rely in estimation heavily on the code written by Alexios Ghalanos.

There is a more complete package than the one I used here, which is more suitable for multivariate estimation [library(rmgarch)]. What I did here has a didactic flavor and is not as efficient as can be.

You might also like:

4 comments on “Multivariate volatility forecasting (1)”

Rob says:

07/13/2015 at 3:08 PM

Super interesting post. Where, in the R Code, is the “TT” variable defined? (that would be the number of rows for the Uvolatility_fit object).

Best,

Rob

1. Eran Raviv says:
  
  07/13/2015 at 4:24 PM
  
  Thanks. Updated the code.
  
Max Caporin says:

07/22/2015 at 6:49 PM

What you have implemented is not a “genuine” DCC but, opposite, an approximation of the DCC model by Engle (2002). In fact, you are not estimating dynamic conditional correlations by maximum likelihood, whether you calibrate them with a rolling estimator.
One of the elements leading to the diffusion of DCC is the possiblity of adopting a multi-stage estimation approach: first the variances on the marginals by univariate GARCH; then, the correlation dynamic which is driven by only two parameters in the scalar DCC representation.
Then, you should anticipate my question: why didn’t you implement the estimation of the DCC model?
If you tackle this issue, I would also suggest to have a look at Aielli (2013), JBES.

1. Eran Raviv says:
  
  07/26/2015 at 6:54 AM
  
  Thanks for the reference. From there (page 287) : “… the joint quasi-maximum-likelihood (QML) estimation of the DCC model is infeasible for large N. As a feasible estimator, Engle (2002) suggested a three-step procedure called DCC estimator.” As you write: first the variances on the marginals by univariate GARCH. In the code, this is “Uvolatility_fit” (U for univariate, second code snippet) and only then accounting for dynamic correlation.