Hyper-parameters are parameters which are not estimated as an integral part of the model. We decide on those parameters but we don’t estimate them within, but rather beforehand. Therefore they are called hyper-parameters, as in “above” sense.
Almost all machine learning algorithms have some hyper-parameters. Data-driven choice of hyper-parameters means typically, that you re-estimate the model and check performance for different hyper-parameters’ configurations. This adds considerable computational burden. One popular approach to set hyper-parameters is based on a grid-search over possible values using the validation set. Faster and simpler ways to intelligently choose hyper-parameters’ values would go a long way in keeping the stretched computational cost at a level you can tolerate.
Enter the paper “Random Search for Hyper-Parameter Optimization” by James Bergstra and Yoshua Bengio, suggesting with a straight face not to use grid-search but instead, look for good values completely at random. This is very counterintuitive, for how can a random guesses within some region compete with systematically covering the same region? What’s the story there?
Below I share the message of that paper, along with what I personally believe is actually going on (and the two are very different).
Random Search for Hyper-Parameter Optimization
This is figure 1 taken directly from the paper:
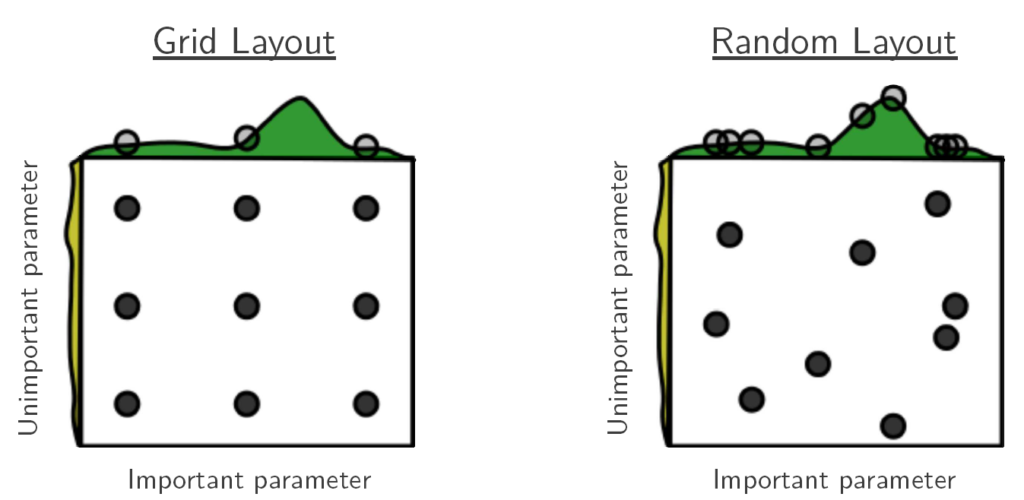
This is schematic view. There are two hyper-parameters to determine. One is important in that it exerts a lot of influence over the final result (x-axis), while the other one is not important in that the final result does not change much for the different values of this hyper-parameter (y-axis with quite flat “influence”). Each point is a trial for two potential hyper-parameter values (9 trials for each of the search strategies). The story this figure tells is that by random search over the region you can end up covering more values along what they call the effective hyper-parameter dimension, at the expense of thoroughly exploring joint-values carefully across all sub-regions (the right figure has no trials at the center of the region).
So, if not all hyper-parameters are born equal, the appeal of random search is in that you can end up covering more values of hyper-parameters which are important, rather focusing your attention equally on all dimensions. A big ‘however’ here is that in real situations we seldom know which hyper-parameters are influential and which are not. I offer a different interpretation of the good results presented in the paper. To aid me I call on two other papers, from related domains that report findings in the same spirit.
Extremely randomized trees
In the usual random forest algorithm the cut-off point for a variable is found based on some accuracy metric (e.g. Gini impurity) with regards to a target. The paper “Extremely randomized trees” (see references) suggests to choose the cut-points randomly, disregarding completely the impact on the target variable. This is weird right? you already chose a variable randomly (say the variable age was randomly chosen), now you also decide randomly on the split (if age > 40 I continue here, if age < 40 I continue there), without looking at your prediction target at all. Think about the gain in speed, instead of systematically creating many splits and looking at the gains in accuracy, you choose only few at random and choose one which looks acceptable. This is similar, not only in spirit, to the previous paper "Random Search for Hyper-Parameter Optimization". Rather than a systematic search, try a few randomly and choose one that has decent performance.
Forecasting Using Random Subspace Methods
In macroeconomic prediction literature it is common to see a lot of information which is condensed by way of principal component analysis, and serves as an input for downstream prediction models. The computation of the principal components rests on a solid numerical procedure which finds the best linear combination of the original variables. Best in the sense that it explains the bulk of variability in the data (see here for an explanation). The paper “Forecasting Using Random Subspace Methods” suggests to, again echoing the other two papers above, rather than estimate the principal components, simply use randomly drawn “principal components”. The authors achieve marked forecasting improvement.
What (do I think) is going on?
So three papers, three different use-cases, three stories, all give the uneasy impression that it is better to randomly guess than to laboriously estimate.
Now for my own take. Paraphrasing John Pierpont Morgan*:
An academic article shares two stories. The one which got it published, and the real one.
It is hard, and perhaps uncalled for, to estimate hyper-parameters which are actually constantly changing. However, academic rigor does not agree with loose-looking statements like “The hyper-parameters will probably not be exactly the same going forward; and even if they will, my estimation efforts can result in hyper-parameters that are completely off the mark. So I don’t spend much time trying to estimate them. Rather, I go with something that looks roughly okay.” But this is the meaning of what we observe empirically, I believe, and it makes sense to me. A decent guess, even based on random choices, will do just fine going forward. Don’t sweat over finding the “correct” hyper-parameters. A random search is faster, simpler, and as we see, does the job.
Below you can find the references for this post.
References
Footnotes
* “A man generally has two reasons for doing a thing. One that sounds good, and a real one”









